
 如圖,在△ABC中,AB=AC,以AC為直徑作⊙O交BC于點D,過點D作EF⊥AB于點F,交AC的延長線于點E.
如圖,在△ABC中,AB=AC,以AC為直徑作⊙O交BC于點D,過點D作EF⊥AB于點F,交AC的延長線于點E.分析 (1)EF與⊙O相切,先根據等腰三角形三線合一得:BD是高線也是中線,由此得OD是△ABC的中位線,
所以OD∥AB,所以OD⊥EF,則EF與⊙O相切;
(2)設圓的半徑為x,根據△EOD∽△EAF,列比例式求x的值,則直徑AC=$\frac{15}{2}$,則AB=$\frac{15}{2}$,由此可得結論.
解答 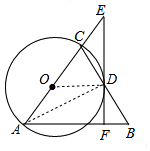 解:(1)EF與⊙O相切,理由是:
解:(1)EF與⊙O相切,理由是:
連接OD、AD,
∵AC是⊙O的直徑,
∴∠ADC=90°,
∵AB=AC,
∴BD=DC,
∵OA=OC,
∴OD為△ABC的中位線,
∴OD∥AB,
∵EF⊥AB,
∴OD⊥EF,
∴EF與⊙O相切;
(2)∵OD∥AB,
∴△EOD∽△EAF,
∴$\frac{OD}{AF}=\frac{OE}{AE}$,
Rt△AEF中,sinE=$\frac{3}{5}$=$\frac{AF}{AE}$,
∵AF=6,
∴$\frac{3}{5}=\frac{6}{AE}$,
∴AE=10,
設OD=x,則OA=OD=x,
∴$\frac{x}{6}=\frac{10-x}{10}$,
x=$\frac{15}{4}$,
∴OA=$\frac{15}{4}$,
∴AC=2OA=$\frac{15}{2}$,
∴AB=AC=$\frac{15}{2}$,
∴BF=AB-AF=$\frac{15}{2}$-6=$\frac{3}{2}$.
點評 本題考查了直線和圓的位置關系、切線的判定、等腰三角形的性質及三角函數的定義,知道直線和圓的三種位置關系:①相離,②相切,③相交;重點掌握相切的判定:邊半徑證垂直或有垂直證半徑.


科目:初中數學 來源: 題型:解答題
 如圖,電信部門要在公路m,n之間的S區域修建一座電視信號發射塔P.按照設計要求,發射塔P到區域S內的兩個城鎮A,B的距離必須相等,到兩條公路m,n的距離也必須相等.發射塔P應建在什么位置?
如圖,電信部門要在公路m,n之間的S區域修建一座電視信號發射塔P.按照設計要求,發射塔P到區域S內的兩個城鎮A,B的距離必須相等,到兩條公路m,n的距離也必須相等.發射塔P應建在什么位置?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖:已知△ABC中,AB=AC,D為AB上一點,過D作DF⊥AB,交AC于E,交BC延長線于點F.求證:∠F=$\frac{1}{2}$∠A.
如圖:已知△ABC中,AB=AC,D為AB上一點,過D作DF⊥AB,交AC于E,交BC延長線于點F.求證:∠F=$\frac{1}{2}$∠A.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
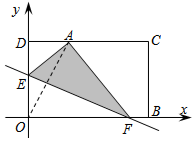 如圖,在平面直角坐標系中,一張矩形紙片OBCD按圖所示放置,已知OB=10,BC=6,將這張紙片折疊,使點O落在CD上,記作點A,折痕與邊OD交于點E,與邊OB交于點F,已知點E的坐標為(0,4),則點A的坐標為(2$\sqrt{3}$,6).
如圖,在平面直角坐標系中,一張矩形紙片OBCD按圖所示放置,已知OB=10,BC=6,將這張紙片折疊,使點O落在CD上,記作點A,折痕與邊OD交于點E,與邊OB交于點F,已知點E的坐標為(0,4),則點A的坐標為(2$\sqrt{3}$,6).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 小華和爸爸上山游玩,爸爸乘電纜車,小華步行,兩人相約在山頂的纜車終點會合.已知小華行走到纜車終點的路程是爸爸乘纜車到山頂的線路長的2倍,爸爸在小華出發后50min才乘上電纜車,電纜車的平均速度為180m/min.設小華出發x(min)行走的路程為y(m),圖中的折線表示小華在整個行走過程中y(m)與x(min)之間的函數關系.
小華和爸爸上山游玩,爸爸乘電纜車,小華步行,兩人相約在山頂的纜車終點會合.已知小華行走到纜車終點的路程是爸爸乘纜車到山頂的線路長的2倍,爸爸在小華出發后50min才乘上電纜車,電纜車的平均速度為180m/min.設小華出發x(min)行走的路程為y(m),圖中的折線表示小華在整個行走過程中y(m)與x(min)之間的函數關系.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com