
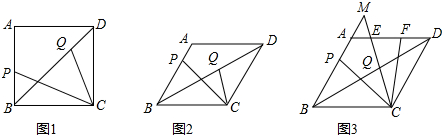
分析 (1)當(dāng)∠BAD=90°時(shí)四邊形ABCD是正方形,易證△APC∽△DQC,則可以得到AP=$\sqrt{2}$DQ,則可求得答案;
(2)作∠QCK=∠PCQ,過(guò)B作BL∥CK,連接AC,易證△DLB∽△DQC則DL=$\sqrt{3}$DQ,然后證明△ACP≌△DCK,即可證得;
(3)設(shè)BC=5k,則MC=7k,過(guò)C作CG⊥AB于G,則∠CGB=90°,在直角△BCG中,利用三角函數(shù)求得BG,CG,然后在直角△MCG中,利用勾股定理求得MG的長(zhǎng),證明△AME∽△DCE,根據(jù)相似三角形的對(duì)應(yīng)邊的比相等求得AE的長(zhǎng),延長(zhǎng)CF、BM交于H,可以證得△DFC∽△AFH,求得AF的長(zhǎng),根據(jù)EF=AF-AE求得k的值,過(guò)C作CN⊥BD于N,證明△EDQ∽△CBQ,求得QD的長(zhǎng),即可求解.
解答 解: (1)如圖1,連接AC,在菱形ABCD中,
(1)如圖1,連接AC,在菱形ABCD中,
∵∠BAD=90°,
∴四邊形ABCD是正方形.
∴∠PCQ=∠CDQ=45°,∠PAC=∠QDC=∠ACD=45°
∴∠ACP+∠ACQ=∠ACQ+∠QCD=45°,
∴∠ACP=∠QCD
∴△APC∽△DQC,
∴$\frac{AP}{DQ}$=$\frac{AC}{CD}$=$\sqrt{2}$;
(2)如圖2,作∠QCK=∠PCQ,過(guò)B作BL∥CK,連接AC.
∵∠QCK=∠ADB,
∴∠CQD=∠CKD
∵CK∥BL,
∴∠CKD=∠BLD,
∴△DLB∽△DQC.
∴DL=$\sqrt{3}$DQ,
∴CD+DK=$\sqrt{3}$DQ,
又∵四邊形APCK對(duì)角互補(bǔ),AC平分∠PAK,
∴△ACP≌△DCK,
∴DK=AP,
∴CD+DK=CD+AP=2CD-BP=$\sqrt{3}$DQ,
即$\sqrt{3}$DQ+BP=2CD;
(3)在菱形ABCD中,∠ABD=∠BDC=30°,
∵∠PCQ=∠ABD=30°,
∴∠PCQ=∠CDQ.
∵BM∥CD,
∴∠PMC=∠DCQ,
∴△DQC∽△MPC
∴CQ:PM=DC:MC=5:7,
∴BC:MC=5:7.
設(shè)BC=5k,則MC=7k,如圖3,過(guò)C作CG⊥AB于G,則∠CGB=90°
∵AD∥BC,
∴∠BAD+∠ABC=180°.
∵∠BAD=120°,
∴∠ABC=60°,
∴BG=$\frac{5}{2}$k,CG=$\frac{5}{2}$$\sqrt{3}$k.
在Rt△MGC中,MG=$\sqrt{M{C}^{2}-C{G}^{2}}$=$\frac{11}{2}$k,
∴BM=8k.
∵AB=BC=5k,
∴AM=BM-AB=3k.
∵AM∥CD,
∴∠AMC=∠DCM,
∵∠AEM=∠DEC,
∴△AME∽△DCE,
∴AM:DC=AE:DE.
∴AE=$\frac{15}{8}$k.
延長(zhǎng)CF、BM交于H,則∠DCF=∠MHC
∵FC平分∠ECD,
∴∠ECF=∠DCF,
∴∠MCH=∠MHC,
∴MH=MC=7k,
∴AH=AM+MH=10k.
∵∠HFA=∠CFD,
∴△DFC∽△AFH,
∴DF:AF=DC:AH
∴AF=$\frac{10}{3}$k,EF=AF-AE=$\frac{35}{24}$k,
∵EF=$\frac{35}{24}$k,
∴k=1.
∴DC=5.
過(guò)C作CN⊥BD于N,
則∠CND=90°.
∵∠CDN=30°,
∴CN=$\frac{5}{2}$,ND=$\frac{5}{2}$$\sqrt{3}$;
∵BC=CD,
∴BD=2ND=5$\sqrt{3}$;
∵∠DQE=∠BQC,∠CBD=∠EDQ,
∴△EDQ∽△CBQ,
∴ED:BC=DQ:QB,
∴QD=$\frac{5}{13}$BD,
∴QD=$\frac{25}{13}$$\sqrt{3}$.
∵2CD-BP=$\sqrt{3}$DQ,
∴BP=$\frac{55}{13}$.
點(diǎn)評(píng) 本題為相似形的綜合應(yīng)用,涉及正方形、菱形的性質(zhì)、相似三角形的判定和性質(zhì)、全等三角形的判定和性質(zhì)、勾股定理、直角三角形的性質(zhì)及方程思想等知識(shí).在(1)中證得△APC∽△DQC是解題的關(guān)鍵,在(2)中構(gòu)造△DLB∽△DQC,證得CD+DK=$\sqrt{3}$DQ是解題的關(guān)鍵,在(3)中利用相似三角形的性質(zhì)求得CD的長(zhǎng)是解題的關(guān)鍵.本題考查知識(shí)點(diǎn)較多,綜合性較強(qiáng),難度較大.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
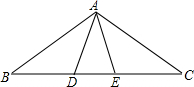 如圖,△ABC中,AB=AC,∠B=∠C,點(diǎn)D,E在BC邊上,添加一個(gè)適當(dāng)?shù)臈l件BE=CD時(shí),可以使△ABE≌△ACD.
如圖,△ABC中,AB=AC,∠B=∠C,點(diǎn)D,E在BC邊上,添加一個(gè)適當(dāng)?shù)臈l件BE=CD時(shí),可以使△ABE≌△ACD.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
 如圖所示,AB∥CD,∠A=∠B,那么下列結(jié)論中不成立的是( )
如圖所示,AB∥CD,∠A=∠B,那么下列結(jié)論中不成立的是( )| A. | ∠A=∠3 | B. | ∠B=∠1 | C. | ∠1=∠3 | D. | ∠2+∠B=180° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖所示,同位角有m對(duì),內(nèi)錯(cuò)角有n對(duì),同旁內(nèi)角有p對(duì).則m+n+p的值是32.
如圖所示,同位角有m對(duì),內(nèi)錯(cuò)角有n對(duì),同旁內(nèi)角有p對(duì).則m+n+p的值是32.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | AB=CD | B. | AD=BC | C. | AB=BC | D. | AC=BD |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,是由每個(gè)邊長(zhǎng)都是1的小正方形構(gòu)成的網(wǎng)格,點(diǎn)O,A,B,M均為格點(diǎn),P為線段OM上的一個(gè)動(dòng)點(diǎn).
如圖,是由每個(gè)邊長(zhǎng)都是1的小正方形構(gòu)成的網(wǎng)格,點(diǎn)O,A,B,M均為格點(diǎn),P為線段OM上的一個(gè)動(dòng)點(diǎn).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | |a|一定是正數(shù) | B. | 倒數(shù)等于它本身的數(shù)只有1 | ||
| C. | 面積為2的正方形的邊長(zhǎng)a是無(wú)理數(shù) | D. | 0是最小的整數(shù) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com