
 如圖,是由每個邊長都是1的小正方形構成的網格,點O,A,B,M均為格點,P為線段OM上的一個動點.
如圖,是由每個邊長都是1的小正方形構成的網格,點O,A,B,M均為格點,P為線段OM上的一個動點.分析 (1)根據勾股定理即可得到結論;
(2)取格點F,E,連接EF,得到點N,取格點S,T,連接ST,得到點R,連接NR即可得到結果.
解答 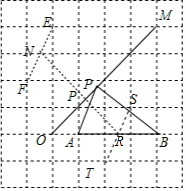 解:(1)點B到OM的距離=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
解:(1)點B到OM的距離=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
故答案為:2$\sqrt{2}$;(2)以點O為原點建立直角坐標系,則A(1,0),B(4,0),設P(a,a),(0≤a≤4),∵PA2=(a-1)2+a2,PB2=(a-4)2+a2,∴PA2+PB2=4(a-$\frac{5}{4}$)2+$\frac{43}{4}$,
∵0≤a≤4,∴當a=$\frac{5}{4}$時,PA2+PB2 取得最小值 $\frac{43}{4}$,
綜上,需作出點P滿足線段OP的長=$\frac{5\sqrt{2}}{4}$;
取格點F,E,連接EF,得到點N,取格點S,T,連接ST,得到點R,連接NR交OM于P,
則點P即為所求.
點評 本題考查了作圖-應用與設計作圖,軸對稱-最短距離問題,正確的作出圖形是解題的關鍵.


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:選擇題
| A. | a=$\sqrt{{a}^{2}}$=($\sqrt{a}$)2 | B. | 若$\sqrt{{a}^{2}}$=a,則a=($\sqrt{a}$)2 | C. | (2$\sqrt{-7}$)2=28 | D. | 2$\sqrt{(-4)^{2}}$=-8 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
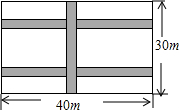 張明的父親打算在院子里種上蔬菜.已知院子是東西長為40m,南北寬為30m的長方形,為了行走方便,要修筑同樣寬的三條道路(如圖),東西方向兩條,南北方向一條.南北方道路垂直于東西道路,余下的部分分別種上蔬菜.若每條道路的寬為1m,求種蔬菜的土地的總面積.
張明的父親打算在院子里種上蔬菜.已知院子是東西長為40m,南北寬為30m的長方形,為了行走方便,要修筑同樣寬的三條道路(如圖),東西方向兩條,南北方向一條.南北方道路垂直于東西道路,余下的部分分別種上蔬菜.若每條道路的寬為1m,求種蔬菜的土地的總面積.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
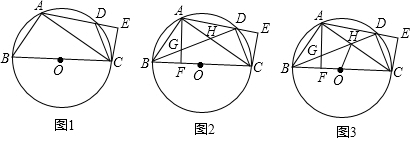
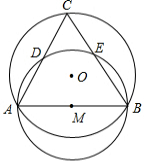 如圖,⊙O的半徑為2,弦AB的長為2$\sqrt{3}$,以AB為直徑作⊙M,點C是優弧$\widehat{AB}$上的一個動點,連接AC、BC,分別交⊙M于點D、E,則線段CD的最大值為2.
如圖,⊙O的半徑為2,弦AB的長為2$\sqrt{3}$,以AB為直徑作⊙M,點C是優弧$\widehat{AB}$上的一個動點,連接AC、BC,分別交⊙M于點D、E,則線段CD的最大值為2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com