
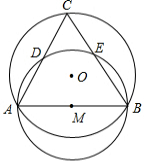
 如圖,⊙O的半徑為2,弦AB的長為2$\sqrt{3}$,以AB為直徑作⊙M,點C是優(yōu)弧$\widehat{AB}$上的一個動點,連接AC、BC,分別交⊙M于點D、E,則線段CD的最大值為2.
如圖,⊙O的半徑為2,弦AB的長為2$\sqrt{3}$,以AB為直徑作⊙M,點C是優(yōu)弧$\widehat{AB}$上的一個動點,連接AC、BC,分別交⊙M于點D、E,則線段CD的最大值為2. 分析 如圖,連接OA、OB、BD.首先證明∠BDC=90°,∠CBD=30°,由此推出CD=$\frac{1}{2}$BC,欲求CD的最大值,只要求出⊙O的弦BC的最大值即可.
解答 解:如圖,連接OA、OB、BD.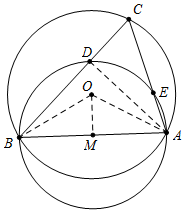
∵OA=OB=2,AM=BM=$\sqrt{3}$.,
∴OM⊥AB,∠AOM=∠BOM,
∴sin∠AOM=$\frac{AM}{AO}$=$\frac{\sqrt{3}}{2}$,
∴∠AOM=60°,
∴∠AOB=2∠AOM=120°,
∴∠C=$\frac{1}{2}$∠AOC=60°,
∵AB是⊙M的直徑,
∴∠ADM=90°,
在Rt△BCD中,∵∠CDB=90°,∠CBD=30°,
∴CD=$\frac{1}{2}$BC,
∴欲求CD的最大值,只要求出⊙O的弦BC的最大值,
∵⊙O的直徑為4,
∴弦BC的最大值為4,
∴CD的最大值為2.
故答案為2.
點評 本題考查圓綜合題、垂徑定理、圓周角定理、直角三角形的30度角性質(zhì)等知識,解題的關(guān)鍵是學會添加輔助線,學會用轉(zhuǎn)化的思想思考問題,本題的突破點是證明CD=$\frac{1}{2}$BC,求出BC的最大值,屬于中考填空題中的壓軸題.


科目:初中數(shù)學 來源: 題型:選擇題
| A. | AB=CD | B. | AD=BC | C. | AB=BC | D. | AC=BD |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,是由每個邊長都是1的小正方形構(gòu)成的網(wǎng)格,點O,A,B,M均為格點,P為線段OM上的一個動點.
如圖,是由每個邊長都是1的小正方形構(gòu)成的網(wǎng)格,點O,A,B,M均為格點,P為線段OM上的一個動點.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
 如圖,四邊形ABCD為矩形,點E在AD邊上,DE=4AE,EF∥AC,交CD邊于點F,連接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,則線段EF的長為$\frac{24}{5}$.
如圖,四邊形ABCD為矩形,點E在AD邊上,DE=4AE,EF∥AC,交CD邊于點F,連接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,則線段EF的長為$\frac{24}{5}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | |a|一定是正數(shù) | B. | 倒數(shù)等于它本身的數(shù)只有1 | ||
| C. | 面積為2的正方形的邊長a是無理數(shù) | D. | 0是最小的整數(shù) |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
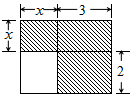 下面四個整式中,不能表示圖中陰影部分面積的是( )
下面四個整式中,不能表示圖中陰影部分面積的是( )| A. | (x+3)(x+2)-2x | B. | x(x+3)+6 | C. | 3(x+2)+x2 | D. | x2+5x |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 了解一批圓珠筆的使用壽命 | |
| B. | 了解全國八年級學生身高的現(xiàn)狀 | |
| C. | 檢查發(fā)射神舟11號飛船的運載火箭的各零部件 | |
| D. | 考察世界人們保護海洋的意識 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | y=2(x+1)2-2 | B. | y=2(x-1)2-2 | C. | y=2(x-2)2-1 | D. | y=2(x+2)2+1 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com