
 如圖,四邊形ABCD為矩形,點(diǎn)E在AD邊上,DE=4AE,EF∥AC,交CD邊于點(diǎn)F,連接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,則線段EF的長(zhǎng)為$\frac{24}{5}$.
如圖,四邊形ABCD為矩形,點(diǎn)E在AD邊上,DE=4AE,EF∥AC,交CD邊于點(diǎn)F,連接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,則線段EF的長(zhǎng)為$\frac{24}{5}$. 分析 作BG⊥EF、延長(zhǎng)EF交BC延長(zhǎng)線于點(diǎn)H,設(shè)AE=x,則DE=4x、AD=BC=5x,證?AEHC得AE=CH=x、證△DEF∽△CHF得$\frac{DF}{CF}$=$\frac{DE}{CH}$=$\frac{4x}{x}$=4,即DF=4CF,即可設(shè)CF=a,則DF=4a,再證△BGC∽△FCH后,設(shè)∠ABE=α,可得∠DEF=∠H=2α,由∠EBG=90°-∠ABE-∠HBG=90°-α-(90°-2α)=α=∠ABE結(jié)合∠BAE=∠BGE=90°、BE=BE,可證△ABE≌△GBE得AB=BG=5a,由$\frac{BG}{BH}=\frac{FC}{FH}$得FH=$\frac{6x}{5}$,根據(jù)勾股定理得FC=$\sqrt{F{H}^{2}-H{C}^{2}}$=$\frac{\sqrt{11}}{5}x$,即a=$\frac{\sqrt{11}}{5}x$,可知AB=5a=$\sqrt{11}$x,在Rt△ABE中由AB2+AE2=BE2得x=1,從而可得DF、DE的長(zhǎng),最后利用勾股定理可得答案.
解答 解:如圖,過(guò)點(diǎn)B作BG⊥EF于點(diǎn)G,延長(zhǎng)EF交BC延長(zhǎng)線于點(diǎn)H,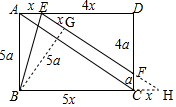
設(shè)AE=x,則DE=4x,AD=BC=5x,
∵AB∥CD,EF∥AC,
∴四邊形AEHC是平行四邊形,
∴AE=CH=x,
∵DE∥CH,
∴△DEF∽△CHF,
∴$\frac{DF}{CF}$=$\frac{DE}{CH}$=$\frac{4x}{x}$=4,即DF=4CF,
設(shè)CF=a,則DF=4a,
又∵∠BGH=∠FCH=90°,∠BHG=∠FHC,
∴△BGC∽△FCH,
設(shè)∠ABE=α,則∠DEF=∠H=2α,
∴∠HBG=90°-∠H=90°-2α,
∴∠EBG=90°-∠ABE-∠HBG=90°-α-(90°-2α)=α=∠ABE,
∵∠BAE=∠BGE=90°,BE=BE,
∴△ABE≌△GBE,
∴AB=BG=5a,
∵$\frac{BG}{BH}=\frac{FC}{FH}$,即$\frac{5a}{6x}=\frac{a}{FH}$,
∴FH=$\frac{6x}{5}$,
則FC=$\sqrt{F{H}^{2}-H{C}^{2}}$=$\sqrt{(\frac{6x}{5})^{2}-{x}^{2}}$=$\frac{\sqrt{11}}{5}x$,即a=$\frac{\sqrt{11}}{5}x$
∴AB=5a=$\sqrt{11}$x,
在Rt△ABE中,由AB2+AE2=BE2得11x2+x2=(2$\sqrt{3}$)2,
解得:x=1或x=-1(舍),
則DF=4a=$\frac{4\sqrt{11}}{5}$x=$\frac{4\sqrt{11}}{5}$,DE=4,
∴EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\frac{24}{5}$,
故答案為:$\frac{24}{5}$.
點(diǎn)評(píng) 本題主要考查相似三角形的判定與性質(zhì)、矩形的性質(zhì)、平行四邊形的判定與性質(zhì)、全等三角形的判定與性質(zhì)及勾股定理等知識(shí)點(diǎn),根據(jù)題中線段的比值及角度的關(guān)系轉(zhuǎn)化為相似問(wèn)題和全等問(wèn)題求解是解題的切入點(diǎn).


 應(yīng)用題天天練四川大學(xué)出版社系列答案
應(yīng)用題天天練四川大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
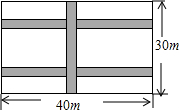 張明的父親打算在院子里種上蔬菜.已知院子是東西長(zhǎng)為40m,南北寬為30m的長(zhǎng)方形,為了行走方便,要修筑同樣寬的三條道路(如圖),東西方向兩條,南北方向一條.南北方道路垂直于東西道路,余下的部分分別種上蔬菜.若每條道路的寬為1m,求種蔬菜的土地的總面積.
張明的父親打算在院子里種上蔬菜.已知院子是東西長(zhǎng)為40m,南北寬為30m的長(zhǎng)方形,為了行走方便,要修筑同樣寬的三條道路(如圖),東西方向兩條,南北方向一條.南北方道路垂直于東西道路,余下的部分分別種上蔬菜.若每條道路的寬為1m,求種蔬菜的土地的總面積.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
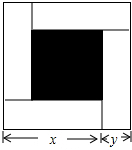 如圖,大正方形的邊長(zhǎng)為m,小正方形的邊長(zhǎng)為n,若用x、y表示四個(gè)長(zhǎng)方形的兩邊長(zhǎng)(x>y),觀察圖案,指出以下關(guān)系式:①x-y=n;②xy=$\frac{{m}^{2}-{n}^{2}}{4}$;③x2-y2=mn;④x2+y2=$\frac{{m}^{2}-{n}^{2}}{2}$.其中正確的關(guān)系式的有①②③.
如圖,大正方形的邊長(zhǎng)為m,小正方形的邊長(zhǎng)為n,若用x、y表示四個(gè)長(zhǎng)方形的兩邊長(zhǎng)(x>y),觀察圖案,指出以下關(guān)系式:①x-y=n;②xy=$\frac{{m}^{2}-{n}^{2}}{4}$;③x2-y2=mn;④x2+y2=$\frac{{m}^{2}-{n}^{2}}{2}$.其中正確的關(guān)系式的有①②③.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
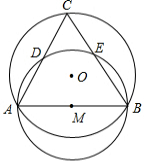 如圖,⊙O的半徑為2,弦AB的長(zhǎng)為2$\sqrt{3}$,以AB為直徑作⊙M,點(diǎn)C是優(yōu)弧$\widehat{AB}$上的一個(gè)動(dòng)點(diǎn),連接AC、BC,分別交⊙M于點(diǎn)D、E,則線段CD的最大值為2.
如圖,⊙O的半徑為2,弦AB的長(zhǎng)為2$\sqrt{3}$,以AB為直徑作⊙M,點(diǎn)C是優(yōu)弧$\widehat{AB}$上的一個(gè)動(dòng)點(diǎn),連接AC、BC,分別交⊙M于點(diǎn)D、E,則線段CD的最大值為2.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com