
 正方形ABCD的邊長(zhǎng)為4,M、N分別是AB、CB上的點(diǎn),MN=4,以MN為直徑做半圓,點(diǎn)P為半圓弧中點(diǎn),點(diǎn)M從點(diǎn)A開(kāi)給滑動(dòng),到點(diǎn)B停止,在這個(gè)運(yùn)動(dòng)過(guò)程中,點(diǎn)P的運(yùn)動(dòng)路徑長(zhǎng)是( )
正方形ABCD的邊長(zhǎng)為4,M、N分別是AB、CB上的點(diǎn),MN=4,以MN為直徑做半圓,點(diǎn)P為半圓弧中點(diǎn),點(diǎn)M從點(diǎn)A開(kāi)給滑動(dòng),到點(diǎn)B停止,在這個(gè)運(yùn)動(dòng)過(guò)程中,點(diǎn)P的運(yùn)動(dòng)路徑長(zhǎng)是( )| A. | 2π | B. | 4-2$\sqrt{2}$ | C. | 8-4$\sqrt{2}$ | D. | 0 |
分析 根據(jù)圖形的運(yùn)動(dòng)的軌跡得出:點(diǎn)P的運(yùn)動(dòng)路徑是兩個(gè)PP′的長(zhǎng),根據(jù)正方形的邊長(zhǎng)為4,得OB=2,則BP=2$\sqrt{2}$,由圖1可知:四邊形MBNP′是矩形,則對(duì)角線NN=BP′=4,可以求PP′的長(zhǎng).
解答 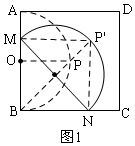 解:在這個(gè)運(yùn)動(dòng)過(guò)程中,點(diǎn)P的運(yùn)動(dòng)路徑分兩個(gè)階段:
解:在這個(gè)運(yùn)動(dòng)過(guò)程中,點(diǎn)P的運(yùn)動(dòng)路徑分兩個(gè)階段:
①點(diǎn)M從A點(diǎn)開(kāi)始運(yùn)動(dòng)到此時(shí)的M時(shí),如圖1,中點(diǎn)P經(jīng)過(guò)的路線為從P到P′的長(zhǎng),即PP′的長(zhǎng),
∵△BOP′是等腰直角三角形,
∵AB=4,
∴OB=OP=2,
∴BP=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∵P為半圓弧的中點(diǎn),MN為半圓的直徑,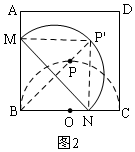
∴MN=BP′=4,
∴PP′=BP′-BP=4-2$\sqrt{2}$;
②當(dāng)點(diǎn)M繼續(xù)運(yùn)動(dòng)到點(diǎn)B時(shí),如圖2,中點(diǎn)P經(jīng)過(guò)的路線為從P′到P的路線長(zhǎng),即也是PP′的長(zhǎng),
綜上所述,點(diǎn)P的運(yùn)動(dòng)路徑長(zhǎng)是:2(4-2$\sqrt{2}$)=8-4$\sqrt{2}$;
故選C.
點(diǎn)評(píng) 本題考查了正方形的性質(zhì)、動(dòng)點(diǎn)的運(yùn)動(dòng)軌跡、圓周角定理、等腰直角三角形的性質(zhì)以及勾股定理,利用數(shù)形結(jié)合的思想,得出P的運(yùn)動(dòng)路線是兩個(gè)PP′的長(zhǎng)是本題的關(guān)鍵.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 3x3•2x2=6x6 | B. | (-x2y)2=x4y | C. | (2x2)3=6x6 | D. | x5÷$\frac{1}{2}$x=2x4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
 如圖,△AOB縮小后得到△COD,△AOB與△COD的相似比是3,若C(1,2),則點(diǎn)A的坐標(biāo)為( )
如圖,△AOB縮小后得到△COD,△AOB與△COD的相似比是3,若C(1,2),則點(diǎn)A的坐標(biāo)為( )| A. | (2,4) | B. | (2,6) | C. | (3,6) | D. | (3,4) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
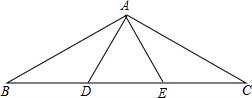 如圖,在△ABC中,AB=AC,∠BAC=120°,點(diǎn)D、E是邊BC的三等分點(diǎn),連接AD、AC.則下列結(jié)論正確的是①②④.
如圖,在△ABC中,AB=AC,∠BAC=120°,點(diǎn)D、E是邊BC的三等分點(diǎn),連接AD、AC.則下列結(jié)論正確的是①②④.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
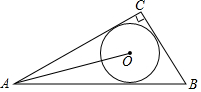 如圖,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的內(nèi)切圓,連接OA,則sin∠OAB的值為( )
如圖,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的內(nèi)切圓,連接OA,則sin∠OAB的值為( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖,已知直線y=$\frac{3}{4}$x-3與x軸、y軸分別交于A、B兩點(diǎn),P是以C(0,2)為圓心,2為半徑的圓上一動(dòng)點(diǎn),連結(jié)PA、PB.則△PAB面積的最大值是13.
如圖,已知直線y=$\frac{3}{4}$x-3與x軸、y軸分別交于A、B兩點(diǎn),P是以C(0,2)為圓心,2為半徑的圓上一動(dòng)點(diǎn),連結(jié)PA、PB.則△PAB面積的最大值是13.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
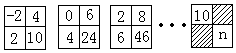
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
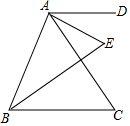 已知,如圖,AD∥BC,AE、BE分別平分∠DAC和∠ABC.若∠DAC=50°,∠ABC=70°,則∠E的度數(shù)是60°.
已知,如圖,AD∥BC,AE、BE分別平分∠DAC和∠ABC.若∠DAC=50°,∠ABC=70°,則∠E的度數(shù)是60°.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com