
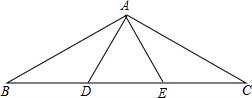
 如圖,在△ABC中,AB=AC,∠BAC=120°,點D、E是邊BC的三等分點,連接AD、AC.則下列結論正確的是①②④.
如圖,在△ABC中,AB=AC,∠BAC=120°,點D、E是邊BC的三等分點,連接AD、AC.則下列結論正確的是①②④.分析 作AM⊥BC于M,DN⊥AB于N,設AB=AC=6,由等腰三角形的性質和三角形內角和定理得出∠B=∠C=30°,由直角三角形的性質得出AM=$\frac{1}{2}$AB=3,BM=CM=$\sqrt{3}$AM=3$\sqrt{3}$,得出BC=2BM=6$\sqrt{3}$,求出BD=DE=CD=2$\sqrt{3}$,DN=$\frac{1}{2}$BD=$\sqrt{3}$,得出BN=$\sqrt{3}$DN=3=$\frac{1}{2}$AB,AN=BN,由線段垂直平分線的性質得出BD=AD,①正確;由等腰三角形的性質得出∠DAN=∠B=30°,同理:CE=AE,∠CAE=∠C=30°,得出AD=DE=AE=2$\sqrt{3}$,△ADE是等邊三角形,③錯誤,④正確,求出∠CAD=90°,②正確;即可得出結論.
解答 解:作AM⊥BC于M,DN⊥AB于N,如圖所示: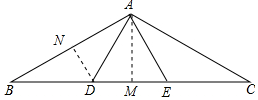
設AB=AC=6,
∵∠BAC=120°,
∴∠B=∠C=30°,
∴AM=$\frac{1}{2}$AB=3,
∴BM=CM=$\sqrt{3}$AM=3$\sqrt{3}$,
∴BC=2BM=6$\sqrt{3}$,
∵點D、E是邊BC的三等分點,
∴BD=DE=CD=2$\sqrt{3}$,
∴DN=$\frac{1}{2}$BD=$\sqrt{3}$,
∴BN=$\sqrt{3}$DN=3=$\frac{1}{2}$AB,
∴AN=BN,
∵DN⊥AB,
∴BD=AD,①正確;
∴∠DAN=∠B=30°,
同理:CE=AE,∠CAE=∠C=30°,
∴AD=DE=AE=2$\sqrt{3}$,△ADE是等邊三角形,③錯誤,④正確,
∴∠DAE=60°,
∴∠CAD=60°+30°=90°,②正確;
故答案為:①②④.
點評 本題考查了等邊三角形的判定與性質、等腰三角形的性質、線段垂直平分線的性質、含30°角的直角三角形的性質、勾股定理等知識;熟練掌握等腰三角形的性質是解決問題的關鍵.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | 3 | C. | -$\frac{4}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,AB是⊙O的直徑,AB=15,AC=9,則tan∠ADC=( )
如圖,AB是⊙O的直徑,AB=15,AC=9,則tan∠ADC=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
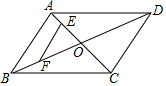 如圖,?ABCD的對角線AC、BD相交于點O,E,F分別是線段AO、BO的中點,若AC+BD=22厘米,△OAB的周長是18厘米,則EF=3.5厘米.
如圖,?ABCD的對角線AC、BD相交于點O,E,F分別是線段AO、BO的中點,若AC+BD=22厘米,△OAB的周長是18厘米,則EF=3.5厘米.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{2}{3}}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{2}{9}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 正方形ABCD的邊長為4,M、N分別是AB、CB上的點,MN=4,以MN為直徑做半圓,點P為半圓弧中點,點M從點A開給滑動,到點B停止,在這個運動過程中,點P的運動路徑長是( )
正方形ABCD的邊長為4,M、N分別是AB、CB上的點,MN=4,以MN為直徑做半圓,點P為半圓弧中點,點M從點A開給滑動,到點B停止,在這個運動過程中,點P的運動路徑長是( )| A. | 2π | B. | 4-2$\sqrt{2}$ | C. | 8-4$\sqrt{2}$ | D. | 0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com