
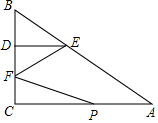
 如圖,在Rt△ABC中,∠C=90°,點D在BC上,點E在AB上,且DE∥AC,AE=5,DE=2,DC=3,動點P從點A出發,沿邊AC以每秒2個單位長的速度向終點C運動,同時動點F從點C出發,在線段CD上以每秒1個單位長的速度向終點D運動,設運動時間為t秒.
如圖,在Rt△ABC中,∠C=90°,點D在BC上,點E在AB上,且DE∥AC,AE=5,DE=2,DC=3,動點P從點A出發,沿邊AC以每秒2個單位長的速度向終點C運動,同時動點F從點C出發,在線段CD上以每秒1個單位長的速度向終點D運動,設運動時間為t秒.分析 (1)作EH⊥AC于H,如圖,易得四邊形CDEH為矩形,從而得到CH=DE=2,EH=CD=3,然后利用勾股定理計算出AH即可得到AC的長;
(2)CF=t,PA=2t,則DF=3-t,CP=6-2t,0<t<3,由于∠C=∠FDE,根據兩組對應邊的比相等且夾角對應相等的兩個三角形相似可分類討論:若$\frac{CF}{DF}$=$\frac{CP}{DE}$時,△CFP∽△DFE,若$\frac{CF}{DE}$=$\frac{CP}{DE}$,則△CFP∽△DEF,然后分別利用相似比得到關于t的方程,再解方程求出t即可.
解答 解:(1)作EH⊥AC于H,如圖,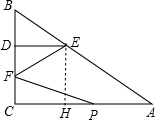 ∵∠C=90°,DE∥AC,
∵∠C=90°,DE∥AC,
∴四邊形CDEH為矩形,
∴CH=DE=2,EH=CD=3,
在Rt△AEH中,AH=$\sqrt{A{E}^{2}-E{H}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AC=CH+AH=2+4=6;
(2)CF=t,PA=2t,則DF=3-t,CP=6-2t,0<t<3,
∵∠C=∠FDE,
∴當$\frac{CF}{DF}$=$\frac{CP}{DE}$時,△CFP∽△DFE,即$\frac{t}{3-t}$=$\frac{6-2t}{2}$,整理得t2-7t+9=0,解得t1=$\frac{7-\sqrt{13}}{2}$,t2=$\frac{7+\sqrt{13}}{2}$(舍去),
∴當$\frac{CF}{DE}$=$\frac{CP}{DE}$時,△CFP∽△DEF,即$\frac{t}{2}$=$\frac{6-2t}{3-t}$,t=4(舍去),
綜上所述,t的值為$\frac{7-\sqrt{13}}{2}$.
點評 本題考查了相似三角形的判定:兩組對應邊的比相等且夾角對應相等的兩個三角形相似.也考查了勾股定理.


科目:初中數學 來源: 題型:解答題
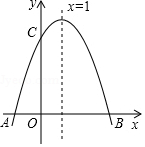 如圖,二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,交y軸于C點,其中B點坐標為(3,0),C點坐標為(0,3),且圖象對稱軸為直線x=1.
如圖,二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,交y軸于C點,其中B點坐標為(3,0),C點坐標為(0,3),且圖象對稱軸為直線x=1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
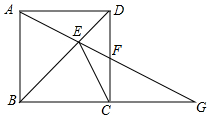 如圖,ABCD是正方形,G是BC延長線上一點,AG交BD于E,交CD于F,求證:CE與△CFG的外接圓相切.
如圖,ABCD是正方形,G是BC延長線上一點,AG交BD于E,交CD于F,求證:CE與△CFG的外接圓相切.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
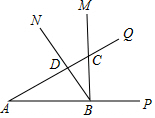 如圖,∠PAQ=∠MBN=30°,∠MBN的頂點B在射線AP上,射線BM和射線BN分別交射線AQ于點C、D,當∠MBN繞點B轉動時.若AB=2$\sqrt{3}$,則CA•CD的最小值是( )
如圖,∠PAQ=∠MBN=30°,∠MBN的頂點B在射線AP上,射線BM和射線BN分別交射線AQ于點C、D,當∠MBN繞點B轉動時.若AB=2$\sqrt{3}$,則CA•CD的最小值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 4 | D. | 12 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com