
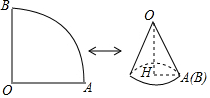
 如圖,已知扇形AOB的圓心角為90°,面積為16π.
如圖,已知扇形AOB的圓心角為90°,面積為16π.分析 (1)首先根據(jù)扇形的面積公式求得扇形的半徑,然后根據(jù)扇形的面積公式S扇形=$\frac{1}{2}$lR(其中l(wèi)為扇形的弧長),求得扇形的弧長.
(2)設(shè)扇形的半徑為R,圓錐的底面圓的半徑為r,先根據(jù)扇形的面積公式解得母線長,再利用弧長公式得到底面半徑r=2,然后利用勾股定理計(jì)算這個(gè)圓錐形桶的高.
解答 解:(1)設(shè)扇形的半徑是R,則$\frac{90π×{R}^{2}}{360}$=16π,
解得:R=8,
設(shè)扇形的弧長是l,則$\frac{1}{2}$lR=16π,即4l=16π,
解得:l=4π.
(2)圓錐的底面圓的半徑為r,
根據(jù)題意得
2πr=$\frac{90π×8}{180}$,解得r=2,
所以個(gè)圓錐形桶的高=$\sqrt{{8}^{2}-{2}^{2}}$=2$\sqrt{15}$.
點(diǎn)評(píng) 本題考查了圓錐的計(jì)算:圓錐的側(cè)面展開圖為一扇形,這個(gè)扇形的弧長等于圓錐底面的周長,扇形的半徑等于圓錐的母線長.也考查了勾股定理.


 暑假作業(yè)暑假快樂練西安出版社系列答案
暑假作業(yè)暑假快樂練西安出版社系列答案 新活力總動(dòng)員暑系列答案
新活力總動(dòng)員暑系列答案 龍人圖書快樂假期暑假作業(yè)鄭州大學(xué)出版社系列答案
龍人圖書快樂假期暑假作業(yè)鄭州大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | a≤b | B. | a<b | C. | a≥b | D. | a>b |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,平面內(nèi)有公共端點(diǎn)的四條射線OA,OB,OC,OD,從射線OA開始按逆時(shí)針方向依次在射線上寫出數(shù)字2,-4,6,-8,10,-12,…則“-2016”在( )上.
如圖,平面內(nèi)有公共端點(diǎn)的四條射線OA,OB,OC,OD,從射線OA開始按逆時(shí)針方向依次在射線上寫出數(shù)字2,-4,6,-8,10,-12,…則“-2016”在( )上.| A. | 射線OA | B. | 射線OB | C. | 射線OC | D. | 射線OD |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,點(diǎn)B在線段AC上,且$\frac{BC}{AB}=\frac{AB}{AC}$,設(shè)AC=1,則AB的長是( )
如圖,點(diǎn)B在線段AC上,且$\frac{BC}{AB}=\frac{AB}{AC}$,設(shè)AC=1,則AB的長是( )| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{3+\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,在⊙O中,AB為直徑,Rt△OBC的直角邊OC=BC=1,過點(diǎn)C作直線DE∥AB交圓于D,E兩點(diǎn),BD與OC交于點(diǎn)F,則∠BDE=15°.
如圖,在⊙O中,AB為直徑,Rt△OBC的直角邊OC=BC=1,過點(diǎn)C作直線DE∥AB交圓于D,E兩點(diǎn),BD與OC交于點(diǎn)F,則∠BDE=15°.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com