
 如圖,在⊙O中,AB為直徑,Rt△OBC的直角邊OC=BC=1,過點C作直線DE∥AB交圓于D,E兩點,BD與OC交于點F,則∠BDE=15°.
如圖,在⊙O中,AB為直徑,Rt△OBC的直角邊OC=BC=1,過點C作直線DE∥AB交圓于D,E兩點,BD與OC交于點F,則∠BDE=15°. 分析 過點O作OG⊥DE于點G,過點C作CH⊥AB于點H,根據(jù)等腰三角形的性質(zhì)求出OG和OD的長度,然后即可求出∠ODG的度數(shù),從而求出答案.
解答 解: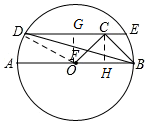 過點O作OG⊥DE于點G,過點C作CH⊥AB于點H,
過點O作OG⊥DE于點G,過點C作CH⊥AB于點H,
∵△OCB是等腰直角三角形,OC=BC=1,
∴由勾股定理可知:OB=$\sqrt{2}$,
∴OD=OB=$\sqrt{2}$,
∴CH=OH=OG=$\frac{\sqrt{2}}{2}$,
∴OD=2OG,
∴∠ODG=30°,
∵DE∥AB,
∴∠ODG=∠DOA=30°,
∴∠ODB=$\frac{1}{2}$∠DOA=15°,
∴∠BDE=∠ODG-∠ODB=15°
故答案為:15°
點評 本題考查圓的綜合問題,涉及含30°的直角三角形的性質(zhì),等腰直角三角形的性質(zhì),垂徑定理、勾股定理,矩形的性質(zhì)等知識,綜合程度較高.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學 來源: 題型:填空題
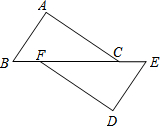 如圖,AB=DE,∠A=∠D=90°,那么要得到△ABC≌△DEF,可以添加一個條件是AC=DF,△ABC與△DEF全等的理由是SAS.
如圖,AB=DE,∠A=∠D=90°,那么要得到△ABC≌△DEF,可以添加一個條件是AC=DF,△ABC與△DEF全等的理由是SAS.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
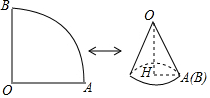 如圖,已知扇形AOB的圓心角為90°,面積為16π.
如圖,已知扇形AOB的圓心角為90°,面積為16π.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 某校九年級為了解學生課堂發(fā)言情況,隨機抽取該年級部分學生,對他們某天在課堂上發(fā)言的次數(shù)進行了統(tǒng)計,其結(jié)果如下表,并繪制了如圖所示的兩幅不完整的統(tǒng)計圖,已知B、E兩組發(fā)言人數(shù)的比為5:2,請結(jié)合圖中相關數(shù)據(jù)回答下列問題:
某校九年級為了解學生課堂發(fā)言情況,隨機抽取該年級部分學生,對他們某天在課堂上發(fā)言的次數(shù)進行了統(tǒng)計,其結(jié)果如下表,并繪制了如圖所示的兩幅不完整的統(tǒng)計圖,已知B、E兩組發(fā)言人數(shù)的比為5:2,請結(jié)合圖中相關數(shù)據(jù)回答下列問題:| 組別 | 課堂發(fā)言次數(shù)n |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 對頂角相等 | B. | 兩直線平行,內(nèi)錯角相等 | ||
| C. | 全等三角形的對應角相等 | D. | 第一象限內(nèi)點的橫坐標是正數(shù) |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 在某市第四次黨代會上,提出了建設美麗城市決勝全面小康的奮斗目標,為策應市委號召,學校決定改造校園內(nèi)的一小廣場,如圖是該廣場的平面示意圖,它是由6個正方形拼成的長方形,已知中間最小的正方形A的邊長是1米.
在某市第四次黨代會上,提出了建設美麗城市決勝全面小康的奮斗目標,為策應市委號召,學校決定改造校園內(nèi)的一小廣場,如圖是該廣場的平面示意圖,它是由6個正方形拼成的長方形,已知中間最小的正方形A的邊長是1米.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com