
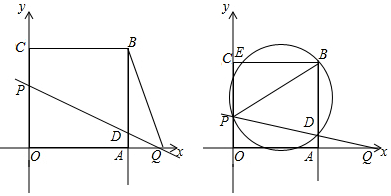
分析 (1)連接PB.依據題意可得到CP=AQ,然后依據正方形的性質可得到BC=AB,∠PCB=∠BAQ=90°,接下來依據SAS可證明△PCB≌△QAB;
(2)設點P的坐標為(0,6-t),則點Q的坐標為(6+t,0).設直線PQ的解析式為y=kx+6-t,將點Q的坐標代入可求得直線PQ的解析式;
(3)當PA=PD時,如圖2所示:連接PB,過點P作PE⊥AB,垂足為E,則四邊形BCPE為矩形,然后用含t的式子,表示出PO、BD的長,從而得到AD的長,然后證明△QDA∽△QPO,接下來,依據相似三角形對應邊成比例列出關于t的方程即可;∴$\frac{AD}{PO}=\frac{AQ}{OQ}$,當t=6時,點D與點A重合,點P與點O重合,此時,△PBD為等腰直角三角形;如圖3所示:當點P位于x軸的下方時,∠PDB為鈍角,可證明△PDB不是等腰三角形此種情況不成立;
(4)連結BQ、PE,過點F作PI⊥OC,垂足為I.由題意可知點P的坐標為(0,6-t),Q的坐標為(6+t,)首先證明△PBQ為等腰直角三角形,于是可證明CE=AD,然后證明PB為∠EPD的角平分線,從而可得到點F在PQ上,接下來,證明△PCE≌△FIP,于是可證明CP=IF=t,PI=AD,將x=6代入直線PQ的解析式求得點D的縱坐標,從而得到AD的長,然后依據OI=PO-PI求得OI的長,從而得到點F的坐標為(t,$\frac{6(6-t)}{6+t}$),設點F的坐標為(x,y),消去字母t得到y與x的函數關系,然后依據點F的軌跡作出判斷即可.
解答 解:(1)如圖1所示:連接PB.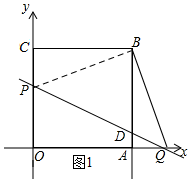
∵點P和點Q運動的速度相同,
∴CP=AQ.
∵四邊形OABC為正方形,
∴BC=AB,∠PCB=∠BAQ=90°.
在△PCB和△QAB中$\left\{\begin{array}{l}{PC=AQ}\\{∠PCB=∠QAB}\\{BC=AB}\end{array}\right.$,
∴△PCB≌△QAB.
(2)設點P的坐標為(0,6-t),則點Q的坐標為(6+t,0).
設直線PQ的解析式為y=kx+6-t.
將點Q的坐標代入得:k(6+t)+6-t=0,解得:k=$\frac{t-6}{t+6}$,
∴直線PQ的解析式為y=$\frac{t-6}{t+6}$x+6-t.(t≥0).
(3)當PA=PD時,如圖2所示:連接PB,過點P作PE⊥AB,垂足為E,則四邊形BCPE為矩形.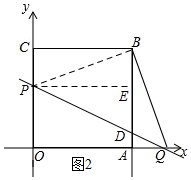
∵四邊形BCPE為矩形,
∴BE=CP=t.
∵PB=PD,PE⊥AB,
∴BE=ED=t,即BD=2t.
∵DA∥PO,
∴△QDA∽△QPO.
∴$\frac{AD}{PO}=\frac{AQ}{OQ}$,即$\frac{6-2t}{6-t}=\frac{t}{6+t}$,解得t=6$\sqrt{2}$-6(負值已舍去).
當t=6時,點D與點A重合,點P與點O重合,此時,△PBD為等腰直角三角形.
如圖3所示:當點P位于x軸的下方時,∠PDB為鈍角.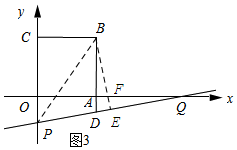
要使△PBD為等腰三角形,則PD=BD.
∴∠PBD=∠BPD.
∵AB∥OC,
∴∠CPB=∠PBD.
∴∠CPB=∠DPB.
∵BC⊥OC,BE⊥PQ,
∴BC=BE=6.
又∵AB=6,BE>AB,
∴假設不成立.
∴當點P位于x軸的下方時,△BPD不能構成等腰三角形.
綜上所述,當t=6$\sqrt{2}$-6或t=6時,△BPD為等腰三角形.
(4)如圖4所示:連結BQ、PE,過點F作PI⊥OC,垂足為I.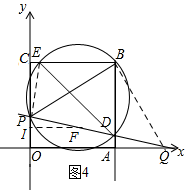
由題意可知點P的坐標為(0,6-t),Q的坐標為(6+t,).
∵∠EBD=90°,
∴DE為圓的直徑.
∴∠EPA=90°.
由(1)可知:△PCB≌△QAB.
∴PB=BQ,∠CBP=∠ABQ.
∴∠CBP+PBD=∠ABQ+∠PBA=90°,即∠PBQ=90°.
∴△PBQ為等腰直角三角形.
∴∠BPQ=45°.
∴PB平分∠EPD.
∴EB=BD.
∴CE=AD.
∵點F與點E關于PB對稱,
∴點F在PB上,且PE=PF.
∵∠CPE+∠CEP=90°,∠IPF+∠CPE=90°,
∴∠CEP=∠IPF.
在△PCE和△FIP中,$\left\{\begin{array}{l}{∠CEP=∠IPF}\\{∠PIF=∠PCE}\\{EP=PF}\end{array}\right.$,
∴△PCE≌△FIP.
∴CP=IF=t,CE=PI.
∴PI=AD.
將x=6代入直線PQ的解析式得:y=$\frac{6(t-6)}{t+6}+6-t$.
∴AD=$\frac{6(t-6)}{t+6}+6-t$.
∴OI=PO-PI=$\frac{6(6-t)}{6+t}$.
設點F的坐標為(x,y),則x=t,y=$\frac{6(6-t)}{6+t}$.
將t=x代入得:y=$\frac{6(6-x)}{6+x}$=$\frac{78}{x+6}-6$,即y=$\frac{78}{x+6}-6$.
∴點F的軌跡為雙曲線的一個部分.
∴第一象限內不存在一個點G,使G到F的距離為定值.
點評 本題主要考查的是圓的綜合應用,解答本題主要應用了全等三角形的性質和判定、相似三角形的性質和判定、圓周角定理以及其推理、軸對稱圖形的性質、等腰直角三角形的性質和判定、角平分線的性質,用含t的式子表示出點F的坐標,然后消去字母t得到點F的縱坐標y與橫坐標x的函數關系式是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
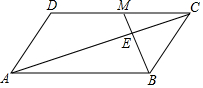 如圖,在?ABCD中,∠ABC的平分線與對角線AC交于點E,與CD交于點M,已知BC=2,DM=3,?ABCD的面積為28,則△ABE的面積為( )
如圖,在?ABCD中,∠ABC的平分線與對角線AC交于點E,與CD交于點M,已知BC=2,DM=3,?ABCD的面積為28,則△ABE的面積為( )| A. | $\frac{28}{3}$ | B. | $\frac{21}{2}$ | C. | 10 | D. | $\frac{14}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\overrightarrow{b}$$∥\overrightarrow{a}$ | B. | |$\overrightarrow{b}$|=3|$\overrightarrow{a}$| | C. | $\overrightarrow{b}$與$\overrightarrow{a}$的方向相反 | D. | 3$\overrightarrow{a}$+$\overrightarrow{b}$=0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com