
分析 (1)根據拋物線與一元二次方程的關系以及勾股定理解答;
(2)運用待定系數法求出經過點C的“蛋圓”切線的解析式;運用二元二次方程組、一元二次方程根的判別式求出過點D的“蛋圓”切線的解析式;
(3)根據題意求出點E的坐標,根據同底等高的兩個三角形面積相等解答;
(4)根據∠BPC=60°保持不變,點P在一圓弧上運動和直徑是最大的弦進行解答即可.
解答 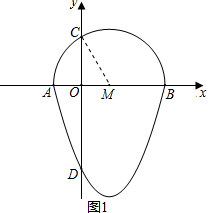 解:(1)當y=0時,x2-2x-3=0,
解:(1)當y=0時,x2-2x-3=0,
解得x1=-1,x2=3,
當x=0時,y=3,
∴A(-1,0),B(3,0),OD=3,
如圖1,連接MC,由題意得,OM=1,MC=2,
∴OC=$\sqrt{M{C}^{2}-O{M}^{2}}$=$\sqrt{3}$,
∴C(0,$\sqrt{3}$),CD=3+$\sqrt{3}$,
故答案為:(-1,0);(3,0);(0,$\sqrt{3}$);3+$\sqrt{3}$;
(2)①如圖2,NC⊥CM,可求得N(-3,0),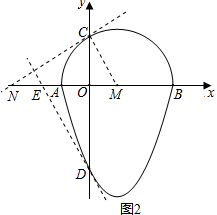
∴經過點C的“蛋圓”切線的解析式為:$y=\frac{{\sqrt{3}}}{3}x+\sqrt{3}$,
②過點D的“蛋圓”切線的解析式為:y=kx-3,
由$\left\{\begin{array}{l}y=kx-3\\ y={x^2}-2x-3\end{array}\right.$,
得:x2-(2+k)x=0,
∵直線與拋物線只有一個交點,
∴k=-2,
∴經過點D的“蛋圓”切線的解析式為:y=-2x-3.
(3)如圖3,∵經過點D的“蛋圓”切線的解析式為:y=-2x-3,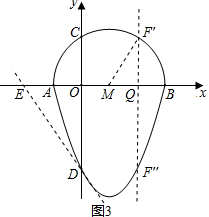 ∴E點坐標為($-\frac{3}{2}$,0),
∴E點坐標為($-\frac{3}{2}$,0),
∵S△CDE=S△CDF,
∴F點的橫坐標為$\frac{3}{2}$,
在Rt△MQF1中可求得F′Q=$\frac{{\sqrt{15}}}{2}$,
把x=$\frac{3}{2}$代入y=x2-2x-3,可求得y=$-\frac{15}{4}$.
∴F′($\frac{3}{2}$,$\frac{{\sqrt{15}}}{2}$),F′′($\frac{3}{2}$,$-\frac{15}{4}$);
(4)如圖4,∵∠BPC=60°保持不變,
因此點P在一圓弧上運動.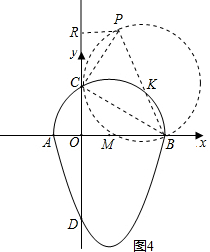 此圓是以K為圓心(K在BC的垂直平分線上,且∠BKC=120°),BK為半徑.
此圓是以K為圓心(K在BC的垂直平分線上,且∠BKC=120°),BK為半徑.
當BP為直徑時,BP最大.
在Rt△PCR中可求得PR=1,RC=$\sqrt{3}$.
所以點P的坐標為(1,2$\sqrt{3}$).
點評 本題考查的是圓與二次函數知識的綜合運用,正確理解“蛋圓”的概念、掌握圓周角定理、二次函數的圖象和性質、靈活運用數形結合思想是解題的關鍵,解答時,注意輔助線的作法要正確.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
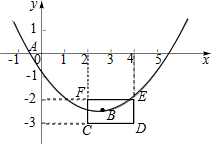 如圖,拋物線y=ax2+bx+c與x軸的一個交點A在點(-1,0)和(0,0)之間(包括這兩點),頂點B是矩形CDEF上(包括邊界和內部)的一個動點,則a的取值范圍是$\frac{2}{25}$≤a≤$\frac{3}{4}$.
如圖,拋物線y=ax2+bx+c與x軸的一個交點A在點(-1,0)和(0,0)之間(包括這兩點),頂點B是矩形CDEF上(包括邊界和內部)的一個動點,則a的取值范圍是$\frac{2}{25}$≤a≤$\frac{3}{4}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 20分 | B. | 22分 | C. | 23分 | D. | 24分 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
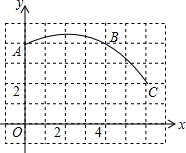 如圖,在單位長度為1的正方形網格中建立一直角坐標系,一條圓弧經過網格點A、B、C,請在網格圖中進行下列操作:
如圖,在單位長度為1的正方形網格中建立一直角坐標系,一條圓弧經過網格點A、B、C,請在網格圖中進行下列操作:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com