

分析 (1)連接BC,根據圓周角定理得到BC是⊙A的直徑,根據勾股定理計算即可求出點B的坐標;
(2)過點P作PD⊥x軸于點D,根據正切的定義求出∠OBC的度數,根據銳角三角函數的定義求出PD、OD,得到點P的坐標;
(3)根據切線長定理求出∠EPB=60°,證明PE∥OD,求出切點E的坐標.
解答 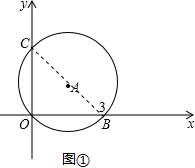 解:(1)如圖①,連接BC,
解:(1)如圖①,連接BC,
∵∠BOC=90°,
∴BC是⊙A的直徑,
∴$BC=2\sqrt{3}$,
∵$C({0,\sqrt{3}})$,
∴$OC=\sqrt{3}$.
∴OB=$\sqrt{B{C}^{2}-O{C}^{2}}$=3,
∴B(3,0);
(2)如圖②,過點P作PD⊥x軸于點D,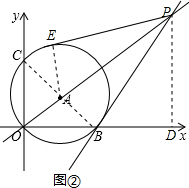
∵PB為⊙A的切線,
$C({0,\sqrt{3}})$,
∴$tan∠OBC=\frac{OC}{OB}=\frac{{\sqrt{3}}}{3}$.
∴∠OBC=30°,
∴∠AOB=30°.
∴∠OPB=180°-∠POB-∠ABO-∠ABP=30°.
∴OB=BP=3,
在Rt△PBD中,∠PDB=90°,∠PBD=60°,BP=3,
∴$BD=\frac{3}{2}$,$PD=\frac{3}{2}\sqrt{3}$.
∵OB=3,
∴$OD=OB+BD=\frac{9}{2}$.
∴$P({\frac{9}{2},\frac{3}{2}\sqrt{3}})$;
(3)由(2)得,∠OPB=30°,
∵PE、PB是⊙A的切線,
∴∠EPA=∠OPB=30°,
∴∠EPB=60°,又∠PBD=60°,
∴PE∥OD,
∴$E({\frac{3}{2},\frac{3}{2}\sqrt{3}})$.
點評 本題考查的是圓的知識的綜合運用,掌握圓周角定理、切線的性質定理以及銳角三角函數的定義是解題的關鍵,解答時,注意輔助線的作法和勾股定理的正確運用.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
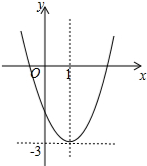 已知二次函數y=ax2+bx+c(a≠0)的圖象如圖,且關于x的一元二次方程ax2+bx+c-m=0沒有實數根,有下列結論:①b2-4ac>0;②abc<0;③m<-3;④3a+b>0.其中,正確結論的個數是( )
已知二次函數y=ax2+bx+c(a≠0)的圖象如圖,且關于x的一元二次方程ax2+bx+c-m=0沒有實數根,有下列結論:①b2-4ac>0;②abc<0;③m<-3;④3a+b>0.其中,正確結論的個數是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
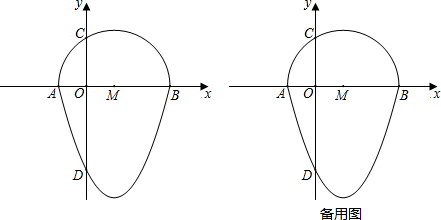
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com