
| 送件數量x(件) | 提成(元/件) |
| 不超過100件的部分 | 1 |
| 超過100件不超過200件的部分 | 1.5 |
| 超過200件的部分 | 2 |
分析 (1)設每個快遞員每天提成為y元,根據提成=送件提成+攬件提成即可得出y關于x的一次函數解析式,根據一次函數的性質即可解決最值問題;
(2)由今年快遞員人數多于28人即可得出關于m的一元一次不等式,解之可得出m的取值范圍,由此即可得出今年每個快遞員送件件數大于210件,根據提成=送件提成+攬件提成求出今年每個快遞員的提成,再根據今年“雙11”期間該片區所有快遞員每天獲得的總提成比去年所有快遞員每天獲得的最大總提成多5000元即可得出關于m的一元二次方程,解之即可得出結論.
解答 解:(1)設每個快遞員每天提成為y元,
根據題意得:y=2(200-x)+100×1+1.5(x-100)=-0.5x+350(150≤x≤200),
∵k=-0.5,
∴y隨著x的增大而減小,
∴當x=150時,y取最大值,最大值為275.
(2)∵今年快遞員人數多于28人,
∴20(1+m%)>28,
解得:m>40,
∴今年每個快遞員每天送件150(1+m%)>210,
∴今年每個快遞員每天提成為100×1+(200-100)×1.5+[150(1+m%)-200]×2+$\frac{50}{2}$×2=3m+200.
根據題意得:20(1+m%)(3m+200)=20×275+5000,
整理得:3m2+500m-32500=0,
解得:m=50或m=-$\frac{650}{3}$(舍去).
答:m的值為50.
點評 本題考查了一次函數的應用、一元二次方程的應用以及解一元一次不等式,解題的關鍵是:(1)根據數量關系提成=送件提成+攬件提成列出y關于x的一次函數關系式;(2)根據今年和去年總提成之間的關系列出關于m的一元二次方程.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | |a+b|的值一定是正數 | B. | a2+1的值一定是正數 | ||
| C. | 當a<b時,a2<b2 | D. | 當a>b時,|a|>|b| |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
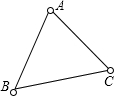 如圖,兔子的三個洞口A、B、C構成△ABC,獵狗想捕捉兔子,必須到三個洞口的距離都相等,則獵狗應蹲守在( )
如圖,兔子的三個洞口A、B、C構成△ABC,獵狗想捕捉兔子,必須到三個洞口的距離都相等,則獵狗應蹲守在( )| A. | 三條邊的垂直平分線的交點 | B. | 三個角的角平分線的交點 | ||
| C. | 三角形三條高的交點 | D. | 三角形三條中線的交點 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,△ABC是一塊銳角三角形材料,邊BC=30cm,高AD=20cm,要把它加工成一個矩形零件,使矩形的一邊在BC上,其余兩個頂點分別在AB,AC上,要使矩形EGHF的面積最大,EF的長應為15cm.
如圖,△ABC是一塊銳角三角形材料,邊BC=30cm,高AD=20cm,要把它加工成一個矩形零件,使矩形的一邊在BC上,其余兩個頂點分別在AB,AC上,要使矩形EGHF的面積最大,EF的長應為15cm.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com