Question

20．甲、乙兩名運動員進行長袍訓練，兩人距終點的路程y（米）與跑步時間x（分）之間的函數圖象如圖1所示（甲為線段AB，乙為折線ACB），根據圖象所提供的信息解答問題：

（1）他們在進行5000米的長跑訓練，甲的速度是250米/分，乙前15分鐘的速度是200米/分；
（2）分別求甲、乙距終點的路程y（米）與跑步時間x（分）之間的函數關系式；
（3）試求x為何值時，兩人相距100米？
（4）若設甲乙兩人之間的距離為s（米），試根據題意在圖2所示的坐標系中繪制出s（米）與跑步時間t（分）之間的函數圖象．

Answer 1

分析 （1）由函數圖象可以得到他們進行的是多少米的長跑訓練和甲的速度和乙前15分鐘的速度分別是多少；
（2）根據函數圖象分別設出各段的函數解析式，根據函數圖象中的數據可以求出各段的函數解析式；
（3）由題意可以知道兩人相距100米有兩種情況，分別寫出相應的關系式即可解答本題；
（4）畫出相應的函數圖象關鍵是求出15鐘時兩人相距最遠，算出這個最遠距離，從而可以畫出相應的函數圖象．

解答 解：（1）由圖象可得，
他們在進行5000米的長跑訓練，甲20分鐘跑了5000米，乙前15分鐘跑了（5000-2000）米，
則甲的速度為：5000÷20=250米/分，乙的速度為：3000÷15=200米/分，
故答案為：5000，250米/分，200米/分；
（2）設線段AC對應的函數解析式為：y=kx+b，
則$\left\{\begin{array}{l}{b=5000}\\{20k+b=0}\end{array}\right.$
解得k=-250，b=5000，
∴線段AC對應的函數解析式是：y=-250x+5000（0≤x≤20）；
設線段AB對應的函數解析式為：y=mx+n，
則$\left\{\begin{array}{l}{n=5000}\\{15m+n=2000}\end{array}\right.$
解得，m=-200，n=5000，
∴線段AB對應的函數解析式是：y=-200x+5000（0≤x≤15），
設線段BC對應的函數解析式為：y=ax+c，
則$\left\{\begin{array}{l}{15a+c=2000}\\{20a+c=0}\end{array}\right.$
解得，a=-400，c=8000，
∴線段BC對應的函數解析式是：y=-400x+8000（15＜x≤20）；
由上可得，甲距終點的路程y（米）與跑步時間x（分）之間的函數關系式是：y=-250x+5000（0≤x≤20）；
乙距終點的路程y（米）與跑步時間x（分）之間的函數關系式是：y=$\left\{\begin{array}{l}{-200x+5000}&{（0≤x≤15）}\\{-400x+8000}&{（15＜x≤20）}\end{array}\right.$；
（3）由題意可得，
-200x+5000-（-250x+5000）=100或-400x+8000-（-250x+5000）=100，
解得，x=2或x=$\frac{58}{3}$，
即當x=2或x=$\frac{58}{3}$，兩人相距100米；
（4）由題意和函數圖象可得，
當x=15時，兩人相距最遠，最遠的距離為：-200×15+5000-（-250×15+5000）=750米，
故s（米）與跑步時間t（分）之間的函數圖象如下圖2所示：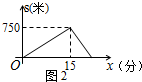
．

點評 本題考查一次函數的應用，解題的關鍵是明確題意，找出所求問題需要的條件即可．