
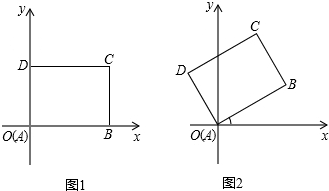
分析 根據旋轉的性質,首先得出OM,DM的長,進而求出ON,NC的長即可得出答案.
解答 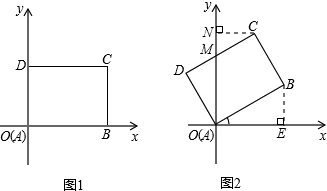 解:∵AB=4,BC=3,
解:∵AB=4,BC=3,
∴圖1中點C的坐標為(4,3),
在圖2中,設CD與y軸交于點M,作CN⊥y軸于點N,那么∠DOM=30°,OD=3,
∴DM=3•tan30°=$\sqrt{3}$,OM=3÷cos30°=2$\sqrt{3}$,
那么CM=4-$\sqrt{3}$,易知∠NCM=30°,
∴MN=CM•sin30°=$\frac{4-\sqrt{3}}{2}$,CN=CM•cos30°=$\frac{4\sqrt{3}-3}{2}$,
則ON=OM+MN=$\frac{3\sqrt{3}+4}{2}$,
∴圖2中C點的坐標為:($\frac{4\sqrt{3}-3}{2}$,$\frac{3\sqrt{3}+4}{2}$).
故答案為:($\frac{4\sqrt{3}-3}{2}$,$\frac{3\sqrt{3}+4}{2}$).
點評 此題考查了矩形的性質以及旋轉問題,關鍵是根據旋轉前后對應角的度數不變,對應線段的長度不變,注意構造直角三角形求解.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
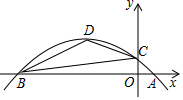 二次函數y=ax2+bx+c 的圖象與x軸交于A(1,0),B兩點,與y軸交于點C,其頂點D的坐標為(-3,2).
二次函數y=ax2+bx+c 的圖象與x軸交于A(1,0),B兩點,與y軸交于點C,其頂點D的坐標為(-3,2).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com