
分析 (1)先根據完全平方公式求出(a+b)2,再求出即可;
(2)兩等式相加、相減,變形后求出a+b=2,再變形后代入a2+b2-2(a+b)=2m,即可求出m.
解答 解:(1)∵a2+b2=5,ab=2,
∴(a+b)2=a2+2ab+b2=5+2×2=9,
∴a+b=±3;
(2)∵a2-2a=m,b2-2b=m,
∴a2-2a=b2-2b,a2-2a+b2-2b=2m,
∴a2-b2-2(a-b)=0,
∴(a-b)(a+b-2)=0,
∵a≠b,
∴a+b-2=0,
∴a+b=2,
∵a2-2a+b2-2b=2m,
∴a2+b2-2(a+b)=2m,
∵a2+b2=5,
∴5-2×2=2m,
解得:m=$\frac{1}{2}$,
即a+b=2,m=$\frac{1}{2}$.
點評 本題考查了分解因式和完全平方公式等知識點,能靈活運用公式進行變形是解此題的關鍵.


 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$$+\sqrt{2}$=2 | B. | 3+$\sqrt{2}$=3$\sqrt{2}$ | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | $\sqrt{9}$+$\sqrt{3}$=3$+\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x=2 | B. | x≠2 | C. | $x=\frac{3}{2}$ | D. | $x≠\frac{3}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
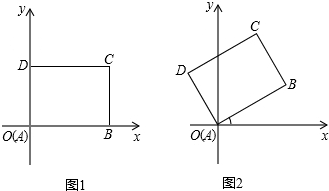
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com