
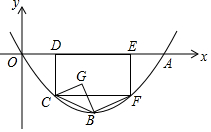
 如圖,在平面直角坐標系中,拋物線y=$\frac{1}{2}$ax2-2ax(a>0)與x軸正半軸交于點A,點B是拋物線的頂點,矩形CDEF的頂點D、E在x正半軸上,C、F在拋物線上,且點D的橫坐標為1,連結(jié)BC、BF,以BC為斜邊向右側(cè)作等腰直角三角形BCG
如圖,在平面直角坐標系中,拋物線y=$\frac{1}{2}$ax2-2ax(a>0)與x軸正半軸交于點A,點B是拋物線的頂點,矩形CDEF的頂點D、E在x正半軸上,C、F在拋物線上,且點D的橫坐標為1,連結(jié)BC、BF,以BC為斜邊向右側(cè)作等腰直角三角形BCG分析 (1)依據(jù)拋物線的對稱軸方程可求得點B的橫坐標為2,將x=2代入拋物線的解析式求得對應(yīng)的y值可求得點B的縱坐標;
(2)依據(jù)拋物線的對稱性可求得點E的坐標,則DE=2,依據(jù)正方形的性質(zhì)可得到DC=2,然后求得點C的縱坐標,最后依據(jù)DC=2可得到關(guān)于a的方程;(3)先求得點G(2,-$\frac{3}{2}$a),由GB=GC可得到BG=1,然后用含a的式子表示BG的長,最后列出關(guān)于a的方程可求得a的值;
(4)當點G在DE上時.先證明△CDG≌△GHB,可得到HG=DC=$\frac{3}{2}$a,DG=HB=2a,然后依據(jù)DG+GH=1列方程求解即可;構(gòu)造等腰直角△ABC,∠C=90°,延長BC到D是BD=AD,可求得∠D=22.5,然后再求得tan22.5°的值,當點G在BF上時,記對稱軸與CF的交點為H,由∠CBG=45°以及拋物線的對稱性可知∠HBF=22.5,然后依據(jù)tan∠FBH=$\frac{FH}{BH}$列方程求解即可.
解答 解:(1)x=-$\frac{b}{2a}$=$\frac{2a}{2×\frac{1}{2}a}$=2,
將x=2代入拋物線的解析式得y=$\frac{1}{2}$a×4-2a×2=-2a.
∴點B的坐標為(2,-2a).
(2)∵D(1,0),拋物線的對稱軸為x=2,
∴E(3,0).
∴DE=2.
∵CDEF為正方形,
∴DC=DE=2.
將x=1代入拋物線的解析式得:y=-$\frac{3}{2}$a,
∴C(1,-$\frac{3}{2}$a).
∴$\frac{3}{2}$a=2,解得:a=$\frac{4}{3}$.
∴拋物線的表達式為y=$\frac{2}{3}$x2-$\frac{8}{3}$x.
(3)如圖1所示:
當點G在對稱軸上時,BG=CG=1.
∵C(1,-$\frac{3}{2}$a),CG∥x軸,
∴G(2,-$\frac{3}{2}$a).
又∵B(2,-2a),
∴BG=$\frac{1}{2}$a=1,解得a=2,
∴拋物線的解析式為y=x2-4x.
(4)如圖2所示:當點G在DE上時.
∵△CGB為等腰直角三角形,
∴CG=BG.
∵∠DGC+∠BGH=90°,∠DCG+∠DGC=90°,
∴∠BGH=∠DCG.
在△CDG和△GHB中$\left\{\begin{array}{l}{∠BGH=∠DCG}\\{∠D=∠H}\\{CG=BG}\end{array}\right.$,
∴△CDG≌△GHB.
∴HG=DC=$\frac{3}{2}$a,DG=HB=2a.
∵DG+GH=1,
∴$\frac{3}{2}$a+2a=1,解得a=$\frac{2}{7}$.
如圖3所示:△ABC為等腰直角三角形,且AB=BD.
∵△ABC為等腰直角三角形,
∴∠ABC=45°,AB=$\sqrt{2}$AC.
∵AB=BD=$\sqrt{2}$AC,
∴∠D=22.5.
∴tan∠22.5=$\frac{AC}{AC+\sqrt{2}AC}$=$\frac{1}{1+\sqrt{2}}$.
如圖4所示:
∵∠CBD=45°,點C與點F關(guān)于BH對稱,
∴∠HBF=22.5°.
∴$\frac{FH}{HB}$=$\frac{1}{1+\sqrt{2}}$,即:$\frac{1}{\frac{1}{2}a}$=$\frac{1}{1+\sqrt{2}}$,解得:a=2$+2\sqrt{2}$.
綜上所述a的值為$\frac{2}{7}$或2+2$\sqrt{2}$.
點評 本題主要考查的是二次函數(shù)的綜合應(yīng)用,解答本題主要應(yīng)用了二次函數(shù)的性質(zhì)、矩形、正方形,等腰直角三角形的性質(zhì),通過構(gòu)造直角三角形求得tan22.5°的值是解題的關(guān)鍵.


科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
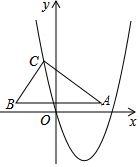 如圖,在平面直角坐標系xOy中,Rt△ABC的直角頂點C在拋物線y=ax2+bx上運動,斜邊AB垂直于y軸,且AB=8,∠ABC=60°,當Rt△ABC的斜邊AB落在x軸上時,B點坐標是(-3,0),A點恰在拋物線y=ax2+bx上
如圖,在平面直角坐標系xOy中,Rt△ABC的直角頂點C在拋物線y=ax2+bx上運動,斜邊AB垂直于y軸,且AB=8,∠ABC=60°,當Rt△ABC的斜邊AB落在x軸上時,B點坐標是(-3,0),A點恰在拋物線y=ax2+bx上查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 5個 | B. | 4個 | C. | 3個 | D. | 2個 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
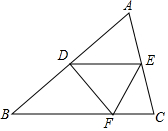 如圖,點D、E分別是邊AB、AC的中點,將△ADE沿著DE對折,點A落在BC邊上的點F,若∠B=50°,則∠BDF的度數(shù)為( )
如圖,點D、E分別是邊AB、AC的中點,將△ADE沿著DE對折,點A落在BC邊上的點F,若∠B=50°,則∠BDF的度數(shù)為( )| A. | 50° | B. | 70° | C. | 75° | D. | 80° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | a+b | B. | a-b | C. | a2-b2 | D. | (a+b)(a2-b2) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
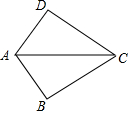 如圖,AB=AD,添加下列一個條件后,仍無法確定△ABC≌△ADC的是( )
如圖,AB=AD,添加下列一個條件后,仍無法確定△ABC≌△ADC的是( )| A. | BC=CD | B. | ∠BAC=∠DAC | C. | ∠B=∠D=90° | D. | ∠ACB=∠ACD |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 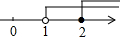 | B. | 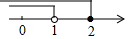 | C. |  | D. |  |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com