

分析 (1)利用同角的余角相等得出∠GDA=∠EDC,進而得出△AGD≌△CED即可‘
(2)先判斷出Rt△DRE≌Rt△DQG得出DR=DQ,進而判斷出Rt△DRH≌Rt△DQH即可得出結論;
(3)方法一、利用三角函數求出DM=$\frac{4}{3}$,即可得出AM=$\frac{8}{3}$.再用勾股定理得出CM=$\frac{3\sqrt{10}}{3}$,最后用勾股定理即可得出結論;
方法二、利用四邊形ACDG的面積直接計算即可得出結論.
解答 解:(1)AG=CE與AG⊥CE均成立.
∵四邊形ABCD、四邊形DEFG是正方形,
∴GD=DE,AD=DC
∵∠GDE=∠ADC=90°,
∴∠GDA=90°-∠ADE=∠EDC.
在△AGD和△CED中,$\left\{\begin{array}{l}{GD=DE}\\{∠GDA=∠EDC}\\{AD=DC}\end{array}\right.$,
∴△AGD≌△CED
∴AG=CE
∴∠GAD=∠ECD
又∵∠HMA=∠DMC.
∴∠AHM=∠ADC=90°.即AG⊥CE
(2)如圖2,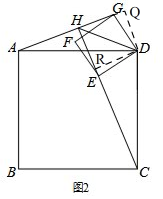 過D作DR⊥HC于R,DQ⊥AG于Q,
過D作DR⊥HC于R,DQ⊥AG于Q,
由(1)知,△AGD≌△CED,
∴∠DEC=∠DGA
∴∠DER=∠DGQ
在Rt△DRE和Rt△DQG中,$\left\{\begin{array}{l}{∠DRE=∠DQG}\\{∠DER=∠DGQ}\\{DE=DQ}\end{array}\right.$
∴Rt△DRE≌Rt△DQG
∴DR=DQ
在Rt△DRH和Rt△DQH中,
∵DR=DQ,DH=DH,∠DRH=∠DQH=90°
∴Rt△DRH≌Rt△DQH
∴∠DHR=∠DHQ
由(1)得AG⊥CE∴∠DHQ=45°.
(3)解法一:如圖3,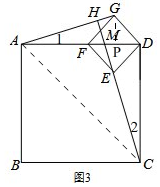 過G作GP⊥AD于P,
過G作GP⊥AD于P,
由題意有,GP=PD=$\sqrt{2}$sin45°=1,
∴AP=3,則tan∠1=$\frac{GP}{AP}=\frac{1}{3}$
而∠1=∠2,
∴tan∠2=$\frac{DM}{DC}$=tan∠1=$\frac{1}{3}$.
∴DM=$\frac{4}{3}$,即AM=AD-DM=$\frac{8}{3}$.
在Rt△DMC中,CM=$\sqrt{C{D}^{2}+D{M}^{2}}$=$\frac{3\sqrt{10}}{3}$,
而△AMH∽△CMD,
∴$\frac{AH}{DC}=\frac{AM}{CM}$,即$\frac{AH}{4}=\frac{\frac{8}{3}}{\frac{4\sqrt{10}}{3}}$,
∴AH=$\frac{4\sqrt{10}}{5}$;
連接AC,顯然有AC=4$\sqrt{2}$,
∴CH=$\sqrt{A{C}^{2}-A{H}^{2}}$=$\frac{8\sqrt{10}}{5}$.
所求CH的長為$\frac{8\sqrt{10}}{5}$
解法二:研究四邊形ACDG的面積
過G作GP⊥AD于P,由題意有GP=PD=$\sqrt{2}$sin45°=1,
∴AP=3,AG=$\sqrt{10}$
而以CD為底邊的三角形CDG的高=PD=1,
S△AGD+S△ACD=S四邊形ACDG=S△ACG+S△CGD,
∴4×1+4×4=$\sqrt{10}$×CH+4×1.
∴CH=$\frac{8\sqrt{10}}{5}$.
點評 此題是四邊形綜合題,主要考查了正方形的性質,全等三角形的判定和性質,勾股定理,銳角三角函數,四邊形的面積的計算方法,解(2)的關鍵是判斷出Rt△DRE≌Rt△DQG,解(3)的關鍵是求出CM=$\frac{3\sqrt{10}}{3}$.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
 如圖ABC中,AB=AC,⊙O為△ABC的外接圍,D為⊙O外一點,∠DCA=∠ACB.
如圖ABC中,AB=AC,⊙O為△ABC的外接圍,D為⊙O外一點,∠DCA=∠ACB.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 6x6÷2x2=3x2 | B. | 8x8÷4x2=2x6 | C. | a3÷a3=0 | D. | $\frac{2}{3}$a5b÷$\frac{3}{2}$a5b=1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
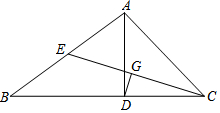 已知:如圖,在△ABC中,AD是BC邊上的高,∠B=30°,∠ACB=45°,CE是AB邊上的中線.
已知:如圖,在△ABC中,AD是BC邊上的高,∠B=30°,∠ACB=45°,CE是AB邊上的中線.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
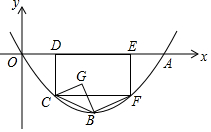 如圖,在平面直角坐標系中,拋物線y=$\frac{1}{2}$ax2-2ax(a>0)與x軸正半軸交于點A,點B是拋物線的頂點,矩形CDEF的頂點D、E在x正半軸上,C、F在拋物線上,且點D的橫坐標為1,連結BC、BF,以BC為斜邊向右側作等腰直角三角形BCG
如圖,在平面直角坐標系中,拋物線y=$\frac{1}{2}$ax2-2ax(a>0)與x軸正半軸交于點A,點B是拋物線的頂點,矩形CDEF的頂點D、E在x正半軸上,C、F在拋物線上,且點D的橫坐標為1,連結BC、BF,以BC為斜邊向右側作等腰直角三角形BCG查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com