Question

5．某大型購物商場在一樓和二樓之間安裝自動扶梯AC，截面如圖所示，一樓和二樓地面平行（即AB所在的直線與CD平行），層高AD為8米，∠ACD=20°，為使得顧客乘坐自動扶梯時不至于碰頭，A、B之間必須達到一定的距離．
（1）要使身高2.26米的姚明乘坐自動扶梯時不碰頭，那么A、B之間的距離至少要多少米？（精確到0.1米）
（2）如果自動扶梯改為由AE、EF、FC三段組成（如圖中虛線所示），中間段EF為平臺（即EF∥DC），AE段和FC段的坡度i=1：2，求平臺EF的長度．（精確到0.1米）
（參考數據：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）

Answer 1

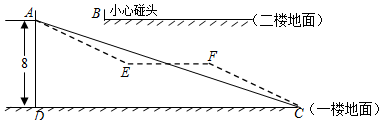
分析 （1）連接AB，作BG⊥AB交AC于點G，在Rt△ABG中，利用已知條件求出AB的長即可；
（2）設直線EF交AD于點P，作CQ⊥EF于點Q，設AP=x，則PE=2x，PD=8-x，在Rt△ACD中利用已知數據可求出CD的長，進而可求出臺EF的長度．

解答 解：（1）連接AB，作BG⊥AB交AC于點G，則∠ABG=90°
∵AB∥CD，∴∠BAG=∠ACD=20°，
在Rt△ABG中，$tan∠BAG=\frac{BG}{AB}$，
∵BG=2.26，tan20°≈0.36，
∴$0.36=\frac{2.26}{AB}$，
∴AB≈6.3，
答：A、B之間的距離至少要6.3米．
（2）設直線EF交AD于點P，作CQ⊥EF于點Q，
∵AE和FC的坡度為1：2，
∴$\frac{AP}{PE}=\frac{CQ}{FQ}=\frac{1}{2}$，
設AP=x，則PE=2x，PD=8-x，
∵EF∥DC，
∴CQ=PD=8-x，
∴FQ=2（8-x）=16-2x，
在Rt△ACD中，$tan∠ACD=\frac{AD}{CD}$，
∵AD=8，∠ACD=20°，
∴CD≈22.22
∵PE+EF+FQ=CD，
∴2x+EF+16-2x=22.22，
∴EF=6.22≈6.2
答：平臺EF的長度約為6.2米．

點評 此題考查了解直角三角形的應用，用到的知識點是坡度角，關鍵是根據題意做出輔助線，構造直角三角形．