

分析 (1)先根據(jù)∠ACB=90°,AC=3,BC=4,求得AB=5,sinA=$\frac{4}{5}$,tanB=$\frac{3}{4}$,再根據(jù)△ACD為直角三角形,求得AD,在Rt△CDE中,求得DE,最后根據(jù)BE=AB-AD-DE進(jìn)行計(jì)算即可;
(2)當(dāng)△CDE時(shí)等腰三角形時(shí),可知∠CDE>∠A>∠B=∠DCE,∠CED>∠B=∠DCE,進(jìn)而得出∠CED=∠CDE,再根據(jù)∠B=∠DCE,∠CDE=∠BDC,得到∠BCD=∠CED=∠CDE=∠BDC,最后求得AD的長(zhǎng);
(3)先作CH⊥AB于H,Rt△ACH中,求得CH和AH的長(zhǎng),在Rt△CDH中,根據(jù)勾股定理得出:CD2=x2-$\frac{18}{5}$x+9,再判定△BDC∽△CDE,得出CD2=DE•DB,即x2-$\frac{18}{5}$x+9=(5-x-y)(5-x),最后求得y關(guān)于x的函數(shù)解析式,并寫出定義域.
解答 (1)在△ABC中,∠ACB=90°,AC=3,BC=4,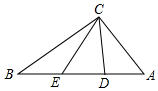
∴AB=5,sinA=$\frac{4}{5}$,tanB=$\frac{3}{4}$,
如圖,當(dāng)CD⊥AB時(shí),△ACD為直角三角形,
∴CD=AC•sinA=$\frac{12}{5}$,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\frac{9}{5}$,
又∵∠DCE=∠ABC,
∴在Rt△CDE中,DE=CD•tan∠DCE=$\frac{12}{5}$×$\frac{3}{4}$=$\frac{9}{5}$,
∴BE=AB-AD-DE=5-$\frac{9}{5}$-$\frac{9}{5}$=$\frac{7}{5}$;
(2)當(dāng)△CDE時(shí)等腰三角形時(shí),可知∠CDE>∠A>∠B=∠DCE,∠CED>∠B=∠DCE,
∴唯有∠CED=∠CDE,
又∵∠B=∠DCE,∠CDE=∠BDC,
∴∠BCD=∠CED=∠CDE=∠BDC,
∴BD=BC=4,
∴AD=5-4=1;
(3)如圖所示,作CH⊥AB于H,
∵$\frac{1}{2}$×BC×AC=$\frac{1}{2}$AB×CH,
∴CH=$\frac{12}{5}$,
∴Rt△ACH中,AH=$\sqrt{A{C}^{2}-C{H}^{2}}$=$\frac{9}{5}$,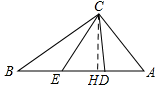
∴在Rt△CDH中,CD2=CH2+DH2=($\frac{12}{5}$)2+($\frac{9}{5}$-x)2=x2-$\frac{18}{5}$x+9,
又∵∠CDE=∠BDC,∠DCE=∠B,
∴△BDC∽△CDE,
∴CD2=DE•DB,
即x2-$\frac{18}{5}$x+9=(5-x-y)(5-x),
解得$y=\frac{32x-80}{5x-25}$$(0<x<\frac{5}{2})$.
點(diǎn)評(píng) 本題屬于三角形綜合題,主要考查了相似三角形的判定與性質(zhì),等腰三角形的性質(zhì),勾股定理以及解直角三角形的綜合應(yīng)用,解決問題的關(guān)鍵是中輔助線構(gòu)造直角三角形,根據(jù)勾股定理以及面積法進(jìn)行求解.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | (3,4) | B. | (1,2) | C. | (3,2) | D. | (1,4) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
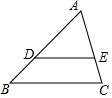 如圖,點(diǎn)D、E位于△ABC的兩邊上,下列條件能判定DE∥BC的是( )
如圖,點(diǎn)D、E位于△ABC的兩邊上,下列條件能判定DE∥BC的是( )| A. | AD•DB=AE•EC | B. | AD•AE=BD•EC | C. | AD•CE=AE•BD | D. | AD•BC=AB•DE |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
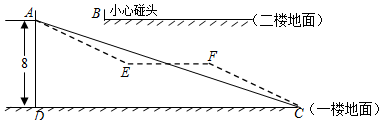
 如圖,小明家所在小區(qū)的前后兩棟樓AB、CD,小明在自己所住樓AB的底部A處,利用對(duì)面樓CD墻上玻璃(與地面垂直)的反光,測(cè)得樓AB頂部B處的仰角是α,若tanα=0.45,兩樓的間距為30米,則小明家所住樓AB的高度是27米.
如圖,小明家所在小區(qū)的前后兩棟樓AB、CD,小明在自己所住樓AB的底部A處,利用對(duì)面樓CD墻上玻璃(與地面垂直)的反光,測(cè)得樓AB頂部B處的仰角是α,若tanα=0.45,兩樓的間距為30米,則小明家所住樓AB的高度是27米.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com