
 已知二次函數y=ax2+bx+c+2的圖象如圖所示,有下列4個結論:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中結論正確的有( )
已知二次函數y=ax2+bx+c+2的圖象如圖所示,有下列4個結論:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中結論正確的有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 ①由拋物線開口向下a>0,拋物線和y軸的正半軸相交,c>0,-$\frac{b}{2a}$<0,b<0,所以abc<0;
②根據拋物線與x軸有一個交點,得到b2-4ac=0,于是得到b2=4ac;
③根據x=-1時,y=a+c-b=0,判斷結論;
⑤根據x=-1時,函數y=a+b+c的值最小,得出當m≠-1時,有a-b+c>am2+bm+c,判斷結論.
解答 解:∵開口向上,∴a>0,
∵拋物線和y軸的正半軸相交,∴c>0,
∵對稱軸為x=-$\frac{b}{2a}$=-1,∴b=2a<0,
∴abc<0,故①正確;
∵拋物線與x軸有一個交點,
∴b2-4ac=0,
∴b2=4ac;故②正確;
∵當x=-1時,a-b+c=0,
∴a+c=b,故③錯誤;
∵當x=-1時,二次函數有最小值,所以當m≠-1時,有a-b+c<am2+bm+c,所以a<m(am+b)+b,故④正確.
故選C.
點評 本題主要考查圖象與二次函數系數之間的關系,會利用對稱軸的范圍求2a與b的關系,以及二次函數與方程之間的轉換的熟練運用.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)如圖,木棒AB位于點光源P和地面CD之間,AB∥CD,若光源P到木棒AB的距離是1米,木棒AB到底面的距離也為1米,測得木棒AB的長度為2米,求木棒AB在地面的影長CD;
(1)如圖,木棒AB位于點光源P和地面CD之間,AB∥CD,若光源P到木棒AB的距離是1米,木棒AB到底面的距離也為1米,測得木棒AB的長度為2米,求木棒AB在地面的影長CD;| 光源P到木棒AB的距離 | 木棒AB在地面的影長 |
| 1米 | 4 |
| 2米 | 3 |
| 3米 | $\frac{8}{3}$ |
| …. | |
| 結論:平行于地面的線段長度一定,到地面的距離一定,則其上方的光源逐漸遠離線段時,該線段在地面上的影長逐漸變小(填“變大”或“變小”). | |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
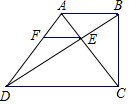 如圖,在四邊形ABCD中,AB∥CD,∠ABC=90°,CD=2AB,對角線AC與BD相交于點E,EF∥CD交AD于點F.
如圖,在四邊形ABCD中,AB∥CD,∠ABC=90°,CD=2AB,對角線AC與BD相交于點E,EF∥CD交AD于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,AB∥CD,∠B=26°,∠D=39°,求∠BED的度數.
如圖,AB∥CD,∠B=26°,∠D=39°,求∠BED的度數.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
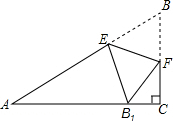 如圖,在△ABC中,∠C=90°,點E,F分別在邊AB,BC上,沿直線EF將△EBF翻折,使頂點B的對應點B1落在AC邊上,且EB1⊥AC.求證:四邊形BFB1E是菱形.
如圖,在△ABC中,∠C=90°,點E,F分別在邊AB,BC上,沿直線EF將△EBF翻折,使頂點B的對應點B1落在AC邊上,且EB1⊥AC.求證:四邊形BFB1E是菱形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com