
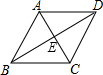
 如圖,要想證明平行四邊形ABCD是菱形,下列條件中不能添加的是( )
如圖,要想證明平行四邊形ABCD是菱形,下列條件中不能添加的是( )| A. | ∠ABD=∠ADB | B. | AC⊥BD | C. | AB=BC | D. | AC=BD |
分析 根據菱形的判定(①有一組鄰邊相等的平行四邊形是菱形,②四條邊都相等的四邊形是菱形,③對角線互相垂直的平行四邊形是菱形)判斷即可.
解答 解:A、∵∠ABD=∠ADB,
∴AB=AD,
∴平行四邊形ABCD是菱形,故本選項不合題意;
B、∵四邊形ABCD是平行四邊形,AC⊥BD,
∴平行四邊形ABCD是菱形,故本選項不合題意;
C、四邊形ABCD是平行四邊形,AB=BC,
∴平行四邊形ABCD是菱形,故本選項不合題意;
D、根據四邊形ABCD是平行四邊形和AC=BD,得出四邊形ABCD是矩形,不能推出四邊形是菱形,故本選項符合題意;
故選:D.
點評 本題考查了菱形的判定定理的應用,注意:菱形的判定定理有①有一組鄰邊相等的平行四邊形是菱形,②四條邊都相等的四邊形是菱形,③對角線互相垂直的平行四邊形是菱形.


科目:初中數學 來源: 題型:解答題
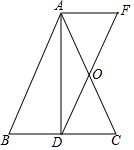 如圖,已知在△ABC中,D為BC上一點,連接AD,過點A作AF∥BC,過點D作DF∥AB,AF與DF交于點F,DF與AC交于點O,若AO=OC.
如圖,已知在△ABC中,D為BC上一點,連接AD,過點A作AF∥BC,過點D作DF∥AB,AF與DF交于點F,DF與AC交于點O,若AO=OC.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 已知二次函數y=ax2+bx+c+2的圖象如圖所示,有下列4個結論:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中結論正確的有( )
已知二次函數y=ax2+bx+c+2的圖象如圖所示,有下列4個結論:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中結論正確的有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{75}$ | B. | $5\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $7\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在每個小正方形邊長為1的方格紙中,△ABC的頂點都在方格紙格點上.
如圖,在每個小正方形邊長為1的方格紙中,△ABC的頂點都在方格紙格點上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某中學課外興趣活動小組準備圍建一個矩形苗圃園,其中一邊靠墻,另外三邊周長為30米的籬笆圍成.已知墻長為18米(如圖所示).回答下列問題:
某中學課外興趣活動小組準備圍建一個矩形苗圃園,其中一邊靠墻,另外三邊周長為30米的籬笆圍成.已知墻長為18米(如圖所示).回答下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com