Question

9．如圖，已知在平面直角坐標系xOy中，二次函數(shù)y=-x²+mx+n的圖象經(jīng)過點A（3，0），B（m，m+1），且與y軸相交于點C．
（1）求這個二次函數(shù)的解析式并寫出其圖象頂點D的坐標；
（2）求∠CAD的正弦值；
（3）設點P在線段DC的延長線上，且∠PAO=∠CAD，求點P的坐標．

Answer 1

分析 （1）根據(jù)二次函數(shù)y=-x²+mx+n的圖象經(jīng)過點A（3，0），B（m，m+1），求得m和n的值即可；
（2）根據(jù)A，C，D三點的坐標，求得CD=$\sqrt{2}$，AC=3$\sqrt{2}$，AD=2$\sqrt{5}$，得到CD²+AC²=AD²，根據(jù)勾股定理的逆定理得出△ACD是直角三角形，且∠ACD=90°，據(jù)此求得∠CAD的正弦值；
（3）先求得直線CD為y=x+3，再設點P的坐標為（a，a+3），然后分兩種情況進行討論：當點P在x軸上方時，過點P作PE⊥x軸于E；當點P在x軸下方時，過點P作PF⊥x軸于F，分別判定△ACD∽△AEP，△ACD∽△AFP，列出比例式求得a的值即可．

解答 解：（1）∵二次函數(shù)y=-x²+mx+n的圖象經(jīng)過點A（3，0），B（m，m+1），
∴$\left\{\begin{array}{l}{0=-9+3m+n}\\{m+1=-{m}^{2}+{m}^{2}+n}\end{array}\right.$，
解得$\left\{\begin{array}{l}{m=2}\\{n=3}\end{array}\right.$，
∴二次函數(shù)的解析式為：y=-x²+2x+3，頂點D的坐標為（1，4）；

（2）如圖所示，在y=-x²+2x+3中，當x=0時，y=3，
∴C（0，3）
∵A（3，0），D（1，4），
∴CD=$\sqrt{2}$，AC=3$\sqrt{2}$，AD=2$\sqrt{5}$，
∴CD²+AC²=AD²，
∴△ACD是直角三角形，且∠ACD=90°，
∴sin∠ACD=$\frac{CD}{AD}$=$\frac{\sqrt{2}}{2\sqrt{5}}$$\frac{{\sqrt{10}}}{10}$；

（3）∵直線CD經(jīng)過C（0，3），D（1，4），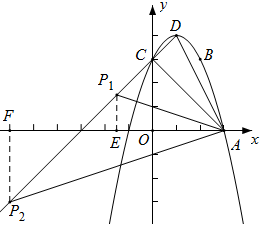
∴設可設直線CD為y=kx+b，則
$\left\{\begin{array}{l}{3=b}\\{4=k+b}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$，
∴直線CD為y=x+3，
設點P的坐標為（a，a+3），
①如圖所示，當點P在x軸上方時，過點P作PE⊥x軸于E，則
PE=a+3，AE=3-a，
∵∠AEP=∠ACD=90°，∠PAO=∠CAD，
∴△ACD∽△AEP，
∴$\frac{PE}{DC}$=$\frac{AE}{AC}$，即$\frac{a+3}{\sqrt{2}}$=$\frac{3-a}{3\sqrt{2}}$，
解得a=-$\frac{3}{2}$，
∴a+3=$\frac{3}{2}$，
∴此時P的坐標為（-$\frac{3}{2}$，$\frac{3}{2}$）；
②如圖所示，當點P在x軸下方時，過點P作PF⊥x軸于F，則
PF=-（a+3），AF=3-a，
∵∠AFP=∠ACD=90°，∠PAO=∠CAD，
∴△ACD∽△AFP，
∴$\frac{PF}{DC}$=$\frac{AF}{AC}$，即$\frac{-a-3}{\sqrt{2}}$=$\frac{3-a}{3\sqrt{2}}$，
解得a=-6，
∴a+3=-3，
∴此時P的坐標為（-6，-3）；
綜上所述，點P的坐標為$（{-\frac{3}{2}，\frac{3}{2}}），（{-6，-3}）$．

點評 本題屬于二次函數(shù)綜合題，主要考查了待定系數(shù)法求函數(shù)解析式、勾股定理的逆定理以及相似三角形的判定與性質(zhì)的綜合應用，解這類問題關鍵是作輔助線構造相似三角形，善于利用幾何圖形的有關性質(zhì)、定理和二次函數(shù)的知識，并注意挖掘題目中的一些隱含條件．