
 如圖,直線AB、CD相交于O,OD平分∠AOF,OE⊥CD于點O,∠1=50°,求∠BOC、∠BOF的度數.
如圖,直線AB、CD相交于O,OD平分∠AOF,OE⊥CD于點O,∠1=50°,求∠BOC、∠BOF的度數.分析 根據垂直的定義,可得∠DOE,根據對頂角的定義,可得∠BOC,根據角平分線的定義,可得∠AOF,根據鄰補角的定義,可得答案.
解答 解:∵OE⊥CD( 已知)
∴∠DOE=90°( 垂直的定義)
∵∠1=50°( 已知)
∴∠AOD=∠EOF-∠1=40°
∵∠BOC與∠AOD為 對頂角角( 對頂角的定義)
∴∠BOC=∠AOD=40°( 對頂角相等)
∵OD平分∠AOF( 已知)
且∠AOD=40°( 已證)
∴∠AOF=2∠AOD=80°( 角平分線的定義)
∵∠BOF+∠AOF=180°( 鄰補角的定義)
∴∠BOF=180°-∠AOF=100°.
點評 本題考查了垂線,利用了垂線的定義,對頂角的性質,角平分線的定義,鄰補角的定義.


科目:初中數學 來源: 題型:選擇題
| A. | 2$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
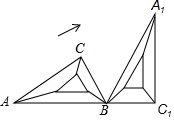 如圖,將三角尺ABC(其中∠ABC=60°,∠C=90°)繞B點按順時針轉動一個角度到A1BCl的位置,使得點A,B,C1在同一條直線上,那么這個旋轉角的度數等于120°.
如圖,將三角尺ABC(其中∠ABC=60°,∠C=90°)繞B點按順時針轉動一個角度到A1BCl的位置,使得點A,B,C1在同一條直線上,那么這個旋轉角的度數等于120°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com