
 如圖,AB為⊙O的直徑,AB=4$\sqrt{3}$,點C為半圓AB上一動點,以BC為邊向⊙O外作正△BCD(點D在直線AB的上方),連接OD,則線段OD的長( )
如圖,AB為⊙O的直徑,AB=4$\sqrt{3}$,點C為半圓AB上一動點,以BC為邊向⊙O外作正△BCD(點D在直線AB的上方),連接OD,則線段OD的長( )| A. | 隨點C的運動而變化,最大值為4 | B. | 隨點C的運動而變化,最大值為4$\sqrt{3}$ | ||
| C. | 隨點C的運動而變化,最小值為2 | D. | 隨點C的運動而變化,但無最值 |
分析 方法一、先利用SSS判斷出△OCD≌△OBD,進而得出點C在運動過程中,∠BDO始終是30°,再構造出直角三角形ODF,即可判斷出點F和點B重合時,OF最大,即可得出OD的最大值.
方法二、先判斷出△COH是等邊三角形,得出HC=OC,∠OCH=60°,進而判斷出△OCD≌△HCB,即可得出OD=BH,由圓中最大的弦是直徑即可得出結論.
解答 解:如圖,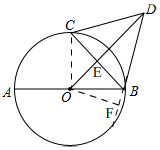 連接OC,
連接OC,
∵△BCD是等邊三角形,
∴∠BDC=60°,CD=BD,
在△OCD和△OBD中,$\left\{\begin{array}{l}{CD=BD}\\{OC=OB}\\{OD=OD}\end{array}\right.$,
∴△OCD≌△OBD(SSS),
∴∠BDO=∠CDO=$\frac{1}{2}$∠BDC=30°,
過點O作OF⊥BD于F,
在Rt△ODF中,∠BDO=30°,
∴OD=2OF,
當點C在運動的過程中,OD要最大,即OF最大,而OF最大=OB,
∴OD最大=2OF最大=2OB=AB=4$\sqrt{3}$.
故選B.
方法二、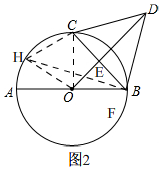 如圖2,連接OC,
如圖2,連接OC,
將△OCD繞點C順時針旋轉60°,則點D落在點B處,OD和⊙O相交于H,
連接OH,CH,
同方法一,得出∠ODC=30°,
∴∠CBH=30°,
∴∠COH=60°,
∴△COH是等邊三角形,
∴HC=OC,∠OCH=60°,
∵△BCD是等邊三角形,
∴CD=BC,∠BCD=60°,
∴∠OCD=∠HCB,
在△OCD和△HCB中,$\left\{\begin{array}{l}{OC=HC}\\{∠OCD=∠HCB}\\{CD=BC}\end{array}\right.$,
∴△OCD≌△HCB(SAS),
∴OD=BH,
∵BH是⊙O的弦,
∴BH最大=AB=4$\sqrt{3}$,
即:OD最大=4$\sqrt{3}$,
故選B.
點評 此題是圓的綜合題,主要考查了等邊三角形的性質和判定,全等三角形的判斷和性質,含30°的直角三角形的性質,解本題的關鍵是構造出直角三角形ODF,判斷出OF最大等于OB.


科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
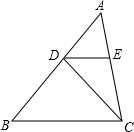 如圖,在△ABC中,AB=4,D是AB上的一點(不與點A、B重合),DE∥BC,交AC于點E,則$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$的最大值為$\frac{1}{4}$.
如圖,在△ABC中,AB=4,D是AB上的一點(不與點A、B重合),DE∥BC,交AC于點E,則$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$的最大值為$\frac{1}{4}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在行駛完某段全程600千米的高速公路時,李師傅對張師傅說:“你的車速太快了,平均每小時比我多跑20千米,比我少用1.5小時就跑完了全程.”
在行駛完某段全程600千米的高速公路時,李師傅對張師傅說:“你的車速太快了,平均每小時比我多跑20千米,比我少用1.5小時就跑完了全程.”查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,點P、Q分別是邊長為4cm的等邊△ABC邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且它們的速度都為1cm/s.設運動時間為t秒,當△PBQ為直角三角形時,t=$\frac{4}{3}$或$\frac{8}{3}$秒.
如圖,點P、Q分別是邊長為4cm的等邊△ABC邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且它們的速度都為1cm/s.設運動時間為t秒,當△PBQ為直角三角形時,t=$\frac{4}{3}$或$\frac{8}{3}$秒.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com