
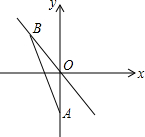
 如圖,A(0,-$\sqrt{2}$),點B為直線y=-x上一動點,當線段AB最短時,點B的坐標為( )
如圖,A(0,-$\sqrt{2}$),點B為直線y=-x上一動點,當線段AB最短時,點B的坐標為( )| A. | (0,0) | B. | (1,-1) | C. | ($\frac{1}{2}$,-$\frac{1}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
分析 根據A(0,-$\sqrt{2}$),點B為直線y=-x上一動點,可知當AB⊥OB時,線段AB最短,作輔助線BC⊥OA于點C,可得OC=CB,由點A(0,-$\sqrt{2}$),可得點B的坐標,從而本題得以解決.
解答 解:∵A(0,-$\sqrt{2}$),點B為直線y=-x上一動點,
∴當AB⊥OB時,線段AB最短,此時點B在第四象限,作BC⊥OA于點C,∠AOB=45°,如下圖所示: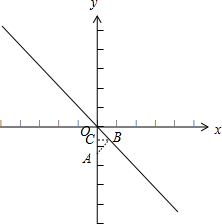
∴OC=CB=$\frac{1}{2}$OA,
∴點B的坐標為($\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}$)
故選D.
點評 本題考查一次函數圖象上點的坐標特征和垂線段最短,解題的關鍵是明確直線外一點到直線的所有線段中垂線段最短,直線y=-x與兩坐標軸的夾角為45°.


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 測試項目 | 測試成績/分 | |
| A | B | |
| 創新 | 85 | 70 |
| 綜合知識 | 50 | 80 |
| 語言 | 88 | 75 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知P、M、N三點,按下面要求畫出圖形;
如圖,已知P、M、N三點,按下面要求畫出圖形;查看答案和解析>>
科目:初中數學 來源: 題型:填空題
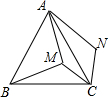 如圖,M為等邊△ABC內部的一點,且MA=8,MB=10,MC=6,將△BMC繞點C順時針旋轉得到△ANC.下列說法中:①MC=NC;②AM=AN;③S四邊形AMCN=S△ABC-S△ABM;④∠AMC=120°.正確的有①③.(請填上番號)
如圖,M為等邊△ABC內部的一點,且MA=8,MB=10,MC=6,將△BMC繞點C順時針旋轉得到△ANC.下列說法中:①MC=NC;②AM=AN;③S四邊形AMCN=S△ABC-S△ABM;④∠AMC=120°.正確的有①③.(請填上番號)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| A | B | C | |
| a | 40 | 10 | 10 |
| b | 3 | 24 | 3 |
| c | 2 | 2 | 6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com