

分析 (1)△ADF為直角三角形,有兩種可能:∠ADF=90°或∠AFD=90°,根據銳角三角函數,分兩種情況進行討論,列方程求解即可;
(2)①根據菱形的判定,可知當AD=DF時,四邊形ADFD′為菱形,根據銳角三角函數列方程求出x,計算菱形的面積即可;②根據三角形中位線定理可知,線段MN掃過的區域的形狀是平行四邊形,其面積為$\frac{24}{5}$.
解答 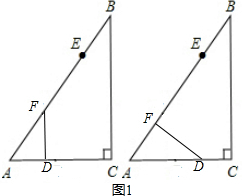 解:(1)∵∠ACB=90°,BC=8,tanA=$\frac{4}{3}$,
解:(1)∵∠ACB=90°,BC=8,tanA=$\frac{4}{3}$,
∴BC=8,AB=10,
∴AD=x,BE=x,AF=6-x,
當∠ADF=90°,如圖1左圖,
∵tanA=$\frac{4}{3}$,
∴cosA=$\frac{3}{5}$,
∴$\frac{AD}{AF}$=$\frac{x}{6-x}$=$\frac{3}{5}$,
∴x=$\frac{9}{4}$;
當∠AFD=90°,如圖1右圖,
∵tanA=$\frac{4}{3}$
∴cosA=$\frac{3}{5}$,
∴$\frac{AF}{AD}$=$\frac{6-x}{x}$=$\frac{3}{5}$,
∴x=$\frac{15}{4}$,
∴當x=$\frac{9}{4}$或$\frac{15}{4}$,△ADF為直角三角形;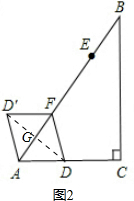 (2)①如圖2,∵AD=AD′,D′F=DF,
(2)①如圖2,∵AD=AD′,D′F=DF,
∴當AD=DF時,四邊形ADFD′為菱形,
∴連接DD′⊥AF于G,AG=$\frac{6-x}{2}$,
∵tanA=$\frac{4}{3}$,
∴cosA=$\frac{3}{5}$,
∴$\frac{AG}{AD}$=$\frac{\frac{6-x}{2}}{x}$=$\frac{3}{5}$,
∴x=$\frac{30}{11}$,
∴S菱形=$\frac{1}{2}$×DD'×AF=$\frac{1}{2}$×$\frac{48}{11}$×$\frac{36}{11}$=$\frac{864}{121}$;
②平行四邊形,$\frac{24}{5}$.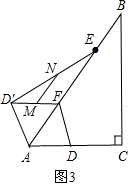
理由:如圖3,∵M、N分別為D′F、D′E的中點,
∴MN∥EF,MN=$\frac{1}{2}$EF=2,
∴線段MN掃過的區域的形狀是平行四邊形,
當D運動到C,則F正好運動到A,此時MA=$\frac{1}{2}$D′A=$\frac{1}{2}$DA=3,
∵∠DAB=∠D′AB,
∴tanA=tan∠D′AB=$\frac{4}{3}$,
設點M到AB的距離為4x,則(3x)2+(4x)2=32,
解得:x=$\frac{3}{5}$,
∴4x=$\frac{12}{5}$,
∴線段MN掃過的區域的面積=2×$\frac{12}{5}$=$\frac{24}{5}$.
故答案為:平行四邊形,$\frac{24}{5}$.
點評 本題屬于四邊形綜合題,主要考查了銳角三角函數、直角三角形的判定、菱形的性質、勾股定理以及三角形中位線性質的綜合運用,具備較強的數形結合能力是解決問題的關鍵.解題時注意分類討論思想和方程思想的運用.


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
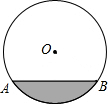 一圓柱形排水管的截面如圖所示,已知排水管的半徑為5m,水面寬AB為8m.由于天氣干燥,水管水面下降,此時排水管水面寬變為6m,求水面下降的高度.
一圓柱形排水管的截面如圖所示,已知排水管的半徑為5m,水面寬AB為8m.由于天氣干燥,水管水面下降,此時排水管水面寬變為6m,求水面下降的高度.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com