Question

9．Rt△ABC中∠C=90°，AC=4，cosB=$\frac{3}{5}$，半徑為r的⊙C與△ABC的邊有兩個交點，則r的取值范圍是0＜r＜2.4．

Answer 1

分析 由題意可知：當AB與⊙C相離時⊙C與△ABC的邊有兩個交點，作CD⊥AB于點D，求得高CD的長，繼而求得答案．

解答 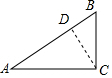解：由題意可知：當AB與⊙C相離時⊙C與△ABC的邊有兩個交點，
∵Rt△ABC中∠C=90°，AC=4，cosB=$\frac{3}{5}$，
∴$\frac{BC}{AB}$=$\frac{3}{5}$，
∴AB=5，BC=3，
作CD⊥AB于點D，
∵$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC
∴CD=$\frac{AC•BC}{AB}$=2.4，
∴半徑為r的⊙C與△ABC的邊有兩個交點，則r的取值范圍是：r＜2.4．
故答案為：0＜r＜2.4．

點評 此題考查了直線與圓的位置關系、勾股定理以及直角三角形的性質．此題難度適中，注意掌握數形結合思想的應用．