
 如圖,△ABC為一個直角三角形的空地,∠C為直角,AC邊長為3百米,BC邊長為4百米,現(xiàn)決定在空地內(nèi)筑一條筆直的路EF(寬度不計),E為BC的中點,F(xiàn)為三角形ABC邊上的一點,且EF將該空地分成一個四邊形和一個三角形,若分成的四邊形和三角形周長相等,求此時小路EF的長度.
如圖,△ABC為一個直角三角形的空地,∠C為直角,AC邊長為3百米,BC邊長為4百米,現(xiàn)決定在空地內(nèi)筑一條筆直的路EF(寬度不計),E為BC的中點,F(xiàn)為三角形ABC邊上的一點,且EF將該空地分成一個四邊形和一個三角形,若分成的四邊形和三角形周長相等,求此時小路EF的長度. 分析 根據(jù)勾股定理得AB=5,由中點的性質(zhì)得BE=EC=2,①當點F在AB上時,設BF=x,則AF=5-x,根據(jù)四邊形和三角形周長相等可求得x的值,作EG⊥BF,由sinB=$\frac{AC}{AB}$=$\frac{3}{5}$、cosB=$\frac{BC}{AB}$=$\frac{4}{5}$求得BG=BEcosB=$\frac{8}{5}$、GE=BEsinB=$\frac{6}{5}$、GF=BF-BG=$\frac{12}{5}$,根據(jù)勾股定理可得EF;②當點F在AC上時,設CF=a,則AF=3-a,由四邊形和三角形周長相等可求得a的值,根據(jù)AF=3-a=-1可排除此種情況.
解答 解:∵AC=3,BC=4,∠C=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵E為BC的中點,
∴BE=EC=2,
①如圖1,當點F在AB上時,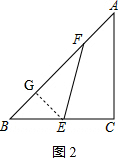
設BF=x,則AF=5-x,
∵BE+BF+EF=EC+AC+AF+EF,即2+x+EF=2+3+5-x+EF,
∴x=4,
過點E作EG⊥BF于點G,
∵sinB=$\frac{AC}{AB}$=$\frac{3}{5}$,cosB=$\frac{BC}{AB}$=$\frac{4}{5}$,
∴BG=BEcosB=2×$\frac{4}{5}$=$\frac{8}{5}$,GE=BEsinB=2×$\frac{3}{5}$=$\frac{6}{5}$,
∴GF=BF-BG=4-$\frac{8}{5}$=$\frac{12}{5}$,
則EF=$\sqrt{G{F}^{2}+G{E}^{2}}$=$\sqrt{(\frac{12}{5})^{2}+(\frac{6}{5})^{2}}$=$\frac{6\sqrt{5}}{5}$(百米);
②如圖2,當點F在AC上時,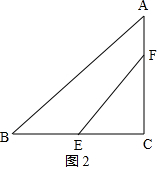
設CF=a,則AF=3-a,
∵EC+CF+EF=BE+EF+AF+AB,即2+a+EF=2+EF+3-a+5,
解得:a=4,
∴此時AF=3-a=-1,不符合題意,舍去;
綜上可知,小路EF的長度為$\frac{6}{5}\sqrt{5}$百米.
點評 本題主要考查勾股定理的應用、解直角三角形等知識點,根據(jù)四邊形與三角形的周長相等分類討論并得到相關線段的長是解題的關鍵.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數(shù)學 來源: 題型:解答題
 如圖,在Rt△ABC中,∠BAC=90°,AG⊥BC于G,BD平分∠ABC,AE⊥BD于H,交BC于E,AG交BD于F,連接EF.求證:
如圖,在Rt△ABC中,∠BAC=90°,AG⊥BC于G,BD平分∠ABC,AE⊥BD于H,交BC于E,AG交BD于F,連接EF.求證:查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
 如圖,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一點O為圓心OA為半徑作⊙O,若⊙O與邊BC始終有交點(包括B、C兩點),則線段AO的取值范圍是$\sqrt{3}≤OA≤\frac{4}{3}\sqrt{3}$.
如圖,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一點O為圓心OA為半徑作⊙O,若⊙O與邊BC始終有交點(包括B、C兩點),則線段AO的取值范圍是$\sqrt{3}≤OA≤\frac{4}{3}\sqrt{3}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 正方形的面積大 | B. | 圓的面積大 | C. | 它們同樣大 | D. | 無法比較 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
 Rt△ABC中∠C=90°,AC=4,cosB=$\frac{3}{5}$,半徑為r的⊙C與△ABC的邊有兩個交點,則r的取值范圍是0<r<2.4.
Rt△ABC中∠C=90°,AC=4,cosB=$\frac{3}{5}$,半徑為r的⊙C與△ABC的邊有兩個交點,則r的取值范圍是0<r<2.4.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
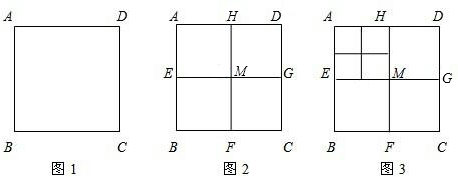
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,二次函數(shù)y=ax2-6ax+4a+3 的圖象與y軸交于點A,點B是x軸上一點,其坐標為(1,0),連接AB,tan∠ABO=2.
如圖,二次函數(shù)y=ax2-6ax+4a+3 的圖象與y軸交于點A,點B是x軸上一點,其坐標為(1,0),連接AB,tan∠ABO=2.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com