

分析 (1)①延長ED到點G使DG=ED,連結GF,GC,就有EF=GF,連結FG、CG,可證△BED≌△CDG,則CG=BE,由三角形的三邊關系就可以得出結論;②由∠A=90°就可以得出∠A+∠ACB=90°,就可以得出∠FCG=90°,由勾股定理就可以得出結論;
(2)延長AC到G使CG=BE,連結DG可以得出△DBE≌△DCG就有DE=DG,∠BDE=∠CDG,由∠BDC=120°,∠EDF=60°,可以得出∠BDE+∠CDF=60°,進而得出∠FDG=60°,就有∠EDF=∠GDF,得出△EDF≌△GDF,得出結論.
解答 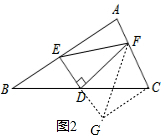 解:(1)①如圖2,延長ED到點G,使DG=ED,連結GF,GC,
解:(1)①如圖2,延長ED到點G,使DG=ED,連結GF,GC,
∵ED⊥DF,
∴EF=GF,
∵D是BC的中點,
∴BD=CD,
在△BDE和△CDG中,
$\left\{\begin{array}{l}{ED=GD}\\{∠BDE=∠GDC}\\{BD=CD}\end{array}\right.$,
∴△DBE≌△DCG(SAS),
∴BE=CG,
∵CG+CF>GF,
∴BE+CF>EF;
②線段BE、CF、EF之間的等量關系為:BE2+CF2=EF2.
證明:如圖2,∵∠A=90°,
∴∠B+∠ACB=90°,
由①可得,△DBE≌△DCG,EF=GF,
∴BE=CG,∠B=∠GCD,
∴∠GCD+∠ACB=90°,即∠GCF=90°,
∴Rt△CFG中,CF2+GC2=GF2,
∴BE2+CF2=EF2;
(2)線段BE、CF、EF之間的數量關系為:EF=BE+CF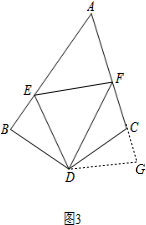 ,
,
理由:如圖3,延長AC到G,使CG=BE,
∵∠B+∠ACD=180°,∠ACD+∠DCG=180°,
∴∠B=∠DCG,
在△DBE和△DCG中,
$\left\{\begin{array}{l}{BE=GC}\\{∠B=∠DCG}\\{BD=CD}\end{array}\right.$,
∴△DBE≌△DCG(SAS),
∴DE=DG,∠BDE=∠CDG,
∵∠BDC=120°,∠EDF=60°,
∴∠BDE+∠CDF=60°,
∴∠CDG+∠CDF=60°,
∴∠EDF=∠GDF,
在△EDF和△GDF中,
$\left\{\begin{array}{l}{DE=DG}\\{∠EDF=∠GDF}\\{DF=DF}\end{array}\right.$,
∴△EDF≌△GDF(SAS),
∴EF=GF,
∵GF=CG+CF,
∴GF=BE+CF,
∴EF=BE+CF.
點評 本題屬于三角形綜合題,主要考查了全等三角形的判定與性質,三角形的三邊關系,勾股定理以及四邊形的性質的綜合運用,解答時作輔助線構造全等三角形,根據線段的和差關系,運用全等三角形對應邊相等進行推導是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
 在行駛完某段全程600千米的高速公路時,李師傅對張師傅說:“你的車速太快了,平均每小時比我多跑20千米,比我少用1.5小時就跑完了全程.”
在行駛完某段全程600千米的高速公路時,李師傅對張師傅說:“你的車速太快了,平均每小時比我多跑20千米,比我少用1.5小時就跑完了全程.”查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
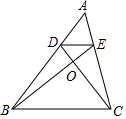 如圖,在△ABC中,點D、E分別在邊AB、AC上,連接CD、BE交于點O,且DE∥BC,OD=1,OC=3,AD=2,則AB的長為( )
如圖,在△ABC中,點D、E分別在邊AB、AC上,連接CD、BE交于點O,且DE∥BC,OD=1,OC=3,AD=2,則AB的長為( )| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com