

分析 (1)①首先求得A、B的坐標,利用方程組求出點C的坐標,②根據三角形的面積公式計算即可;
(2)當A、Q、H在同一直線上,且AH⊥OC時,AQ+HQ最小.即AQ+PQ存在最小值,求得OC的長,利用三角形的面積公式即可求得AQ+PQ的最小值.
解答 解(1)①在y=-2x+8中,令y=0,解得:x=4,
令x=0,解得:y=8,
則A的坐標是(4,0),B的坐標是(0,8),
由$\left\{\begin{array}{l}{y=\frac{6}{5}x}\\{y=-2x+8}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=3}\end{array}\right.$,
∴C($\frac{5}{2}$,3),
②∵A(4,0),B(0,8),C($\frac{5}{2}$,3),
∴S△OAC=$\frac{1}{2}$×4×3=6.
(2)存在.
由題意,在OC上截取OH=OP,連結HQ,
∵OP平分∠AOC,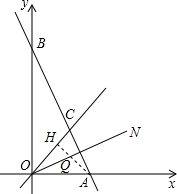
∴∠AOQ=∠COQ,
在△POQ和△HOQ中,
$\left\{\begin{array}{l}{OH=OP}\\{∠HOQ=∠POQ}\\{OQ=OQ}\end{array}\right.$,
∴△POQ≌△HOQ(SAS),
∴PQ=HQ,
∴AQ+PQ=AQ+HQ,
當A、Q、H在同一直線上,且AH⊥OC時,AQ+HQ最小.即AQ+PQ存在最小值.
∵S△ABC=$\frac{1}{2}$•OA×h=5,解得h=$\frac{5}{2}$,
∴點C的縱坐標為$\frac{5}{2}$,
∴點C橫坐標為$\frac{25}{12}$,
∴C($\frac{25}{12}$,$\frac{5}{2}$),
∴OC=$\frac{5\sqrt{61}}{12}$,
∴$\frac{1}{2}$•OC•AH=5,
∴AH=$\frac{24\sqrt{61}}{61}$
∴這個最小值為 $\frac{24\sqrt{61}}{61}$.
點評 本題考查一次函數綜合題、三角形的面積、全等三角形的判定和性質、垂線段最短等知識,解題的關鍵是學會用轉化的思想思考問題,學會利用方程組確定兩個函數圖象的交點坐標,屬于中考常考題型.


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
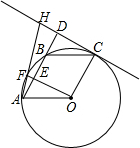 如圖A、F、B、C是半圓O上的四個點,四邊形OABC是平行四邊形,∠FAB=15°,連接OF交AB于點E,過點C作OF的平行線交AB的延長線于點D,延長AF交直線CD于點H.
如圖A、F、B、C是半圓O上的四個點,四邊形OABC是平行四邊形,∠FAB=15°,連接OF交AB于點E,過點C作OF的平行線交AB的延長線于點D,延長AF交直線CD于點H.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com