
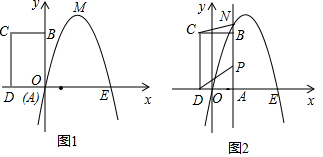
分析 (1)利用頂點坐標假設出解析式,進而將(0,0)代入得出解析式即可;
(2)①根據題意得出P點坐標,進而表示出N點坐標,進而利用當PN=0,即t=0或t=3時,P、N、C、D所構成的多邊形為三角形,求出面積即可,再利用當PN≠0時,P、N、C、D四點所構成的多邊形是四邊形,求出面積即可,即可得出最值;
②分別以Q,M為直角頂點去分析求解即可求得答案.
解答 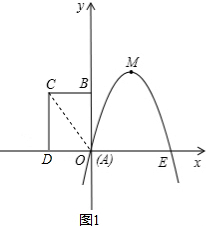 解:(1)設所求函數關系式為y=a(x-2)2+4,
解:(1)設所求函數關系式為y=a(x-2)2+4,
把(0,0)代入解析式得a(0-2)2+4=0,
解得,a=-1,
故函數解析式為y=-(x-2)2+4,
整理得y=-x2+4x.
(2)存在.
①∵將矩形ABCD以每秒1個單位長度的速度從左圖所示位置沿x軸的正方向勻速平行移動;
同時AB上一動點P也以相同的速度從點A出發向B勻速運動,設它們的運動時間為t秒,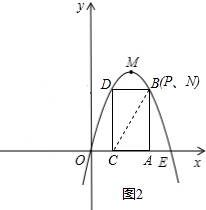 依題意,點P的坐標為:(t,t),點N的坐標為:(t,-t2+4t),
依題意,點P的坐標為:(t,t),點N的坐標為:(t,-t2+4t),
故PN=-t2+3t,
則有:當PN=0,
即t=0或t=3時,分別如圖1,2,
P、N、C、D所構成的多邊形為三角形,
此時S=$\frac{1}{2}$DC•AD=$\frac{1}{2}$×3×2=3,
當PN≠0時,如圖3,
P、N、C、D四點所構成的多邊形是四邊形,
∵PN∥CD,AD⊥DC,
∴S=$\frac{1}{2}$(CD+PN)•AD,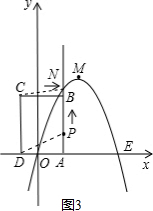 =$\frac{1}{2}$[3+(-t2+3t)]×2,
=$\frac{1}{2}$[3+(-t2+3t)]×2,
=-t2+3t+3,
=-(t-$\frac{3}{2}$)2+$\frac{21}{4}$(0≤t≤3),
∴當t=$\frac{3}{2}$時,S最大=$\frac{21}{4}$>3,
綜上可知P、N、C、D所構成的多邊形的面積S有最大值,這個最大值為:$\frac{21}{4}$;
②如圖4,作點M作MG⊥AB于點G,作MH⊥x軸于點H,
∵M(2,4),E(4,0),
則EH=2,MH=4,MG=2-1=1,
設點Q的坐標為(1,m),
若∠QME=90°,則△MGQ∽△MHE,
∴MG:GQ=MH:EH,
∴1:GQ=4:2,
解得:GQ=0.5,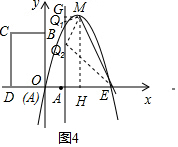 ∴m=4-0.5=3.5,
∴m=4-0.5=3.5,
∴點Q的坐標為(1,3.5);
若∠MQE=90°,則△MGQ∽△QAE,
∴MG:GQ=AQ:AE,
∴1:(4-m)=m:3,
解得:m=1或m=3,
∴點Q的坐標為(1,1)或(1,3);
若∠QEM=90°,則點Q在BA的延長線上,不符合題意.
綜上所述:點Q的坐標為:(1,3.5),(1,1),(1,3).
點評 此題屬于二次函數的綜合題.考查了待定系數求函數解析式的知識、平移問題、矩形的性質以及相似三角形的判定與性質等知識.注意掌握分類討論思想的應用是解此題的關鍵.


 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
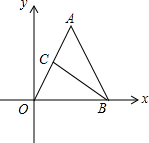 如圖,在直角坐標系中有一個等腰△AOB,點O為坐標原點,AO=AB,OB=4,tan∠AOB=2,點C是線段OA的中點.
如圖,在直角坐標系中有一個等腰△AOB,點O為坐標原點,AO=AB,OB=4,tan∠AOB=2,點C是線段OA的中點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
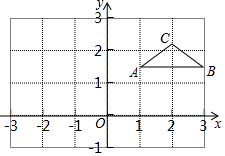 如圖,△ABC在平面直角坐標系內,它的三個頂點的坐標分別為A(1,$\sqrt{2}$),B(3,$\sqrt{2}$),C(2,$\sqrt{5}$),求△ABC的面積.
如圖,△ABC在平面直角坐標系內,它的三個頂點的坐標分別為A(1,$\sqrt{2}$),B(3,$\sqrt{2}$),C(2,$\sqrt{5}$),求△ABC的面積.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com