
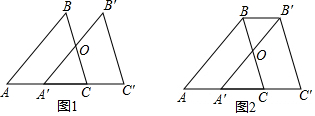
分析 (1)根據AB∥A'B',得到∠A=∠B′A′C′,根據相似三角形的性質得到∠ACB=∠C′由平行線的判定即可得到結論;
(2)由平移的性質得到BC=B′C′,BB′=CC′=3cm,即可得到結論.
解答 解:(1)BC與B'C'平行,
理由:∵AB∥A'B',
∴∠A=∠B′A′C′,
∵∠B=∠B',
∴△ABC∽△A′B′C′,
∴∠ACB=∠C′
∴BC∥B'C';
(2)∵將△ABC沿邊AC向右平移3 cm得到△A'B'C',
∴BC=B′C′,BB′=CC′=3cm,
∴四邊形ABB'C'的周長=AB+AC+B′C′+B′B+CC′=AB+AC+BC+6,
∵△ABC的周長為16 cm,
∴四邊形ABB'C'的周長=22cm.
點評 本題考查了平移的性質,平行線的判定和性質,熟練掌握平移的性質是解題的關鍵.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:選擇題
| A. | 6 | B. | -6 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 13個 | B. | 12個 | C. | 16個 | D. | 15個 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
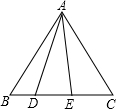 在等邊三角形ABC中,點D在BC上,且BD:DC=1:4,連接DA,作∠DAE,滿足∠DAE=30°,則tan∠BAE的值是$\frac{\sqrt{3}}{2}$.
在等邊三角形ABC中,點D在BC上,且BD:DC=1:4,連接DA,作∠DAE,滿足∠DAE=30°,則tan∠BAE的值是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$(環) | 8.4 | 8.6 | 8.6 | 7.6 |
| S2 | 0.74 | 0.56 | 0.94 | 1.92 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com