
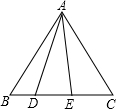
 在等邊三角形ABC中,點D在BC上,且BD:DC=1:4,連接DA,作∠DAE,滿足∠DAE=30°,則tan∠BAE的值是$\frac{\sqrt{3}}{2}$.
在等邊三角形ABC中,點D在BC上,且BD:DC=1:4,連接DA,作∠DAE,滿足∠DAE=30°,則tan∠BAE的值是$\frac{\sqrt{3}}{2}$. 分析 在△ABC外作∠BAF=30°,∵∠DAE=30°,得到∠BAF=∠DAE,過D作DF⊥AF于F,DG⊥AC于G,過B作BH⊥AC于H,設△ABC的邊長為a,求得BH=$\frac{\sqrt{3}}{2}$a,推出四邊形AFDG是矩形,根據矩形的性質得到AF=DG,DF=AG,根據平行線分線段成比例定理得到$\frac{HG}{CH}=\frac{BD}{BC}$=$\frac{1}{5}$,得到AG=$\frac{a}{2}$+$\frac{a}{10}$=$\frac{3}{5}$a=DF,根據三角函數的定義即刻得到結論.
解答  解:在△ABC外作∠BAF=30°,
解:在△ABC外作∠BAF=30°,
∵∠DAE=30°,
∴∠BAF=∠DAE,過D作DF⊥AF于F,DG⊥AC于G,過B作BH⊥AC于H,
設△ABC的邊長為a,
則BH=$\frac{\sqrt{3}}{2}$a,
∵BD:DC=1:4,
∴$\frac{DG}{BH}$=$\frac{CD}{BC}$=$\frac{4}{5}$,
∴DG=$\frac{4}{5}$BH=$\frac{2\sqrt{3}}{5}$a,
∵∠F=∠FAG=∠AGD=90°,
∴四邊形AFDG是矩形,
∴AF=DG,DF=AG,
∴AF=$\frac{2\sqrt{3}}{5}$a,
∵DG∥BH,
∴$\frac{HG}{CH}=\frac{BD}{BC}$=$\frac{1}{5}$,
∴HG=$\frac{1}{5}$CH=$\frac{a}{10}$,
∴AG=$\frac{a}{2}$+$\frac{a}{10}$=$\frac{3}{5}$a=DF,
∴tan∠BAE=tan∠DAF=$\frac{\frac{3}{5}a}{\frac{2\sqrt{3}}{5}a}$=$\frac{\sqrt{3}}{2}$.
故答案為:$\frac{\sqrt{3}}{2}$.
點評 本題考查了平行線分線段成比例定理,矩形的判定和性質,解直角三角形,正確的作出輔助線是解題的關鍵.


 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:初中數學 來源: 題型:填空題
 如圖,在直角坐標系中,直線l與y軸正半軸所夾的銳角為60°,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1,以A1B、BA為鄰邊作?ABA1C1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2,以A2B1、B1A1為鄰邊作?A1B1A2C2;…;按此作法繼續下去,則C3的坐標是(-16$\sqrt{3}$,64);Cn的坐標是(-22(n-1)$\sqrt{3}$,22n)(n為正整數).
如圖,在直角坐標系中,直線l與y軸正半軸所夾的銳角為60°,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1,以A1B、BA為鄰邊作?ABA1C1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2,以A2B1、B1A1為鄰邊作?A1B1A2C2;…;按此作法繼續下去,則C3的坐標是(-16$\sqrt{3}$,64);Cn的坐標是(-22(n-1)$\sqrt{3}$,22n)(n為正整數).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
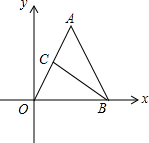 如圖,在直角坐標系中有一個等腰△AOB,點O為坐標原點,AO=AB,OB=4,tan∠AOB=2,點C是線段OA的中點.
如圖,在直角坐標系中有一個等腰△AOB,點O為坐標原點,AO=AB,OB=4,tan∠AOB=2,點C是線段OA的中點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
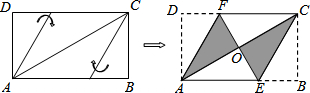 將矩形紙片ABCD按如圖所示的方式折疊,得到菱形AECF.若AB=3,則BC的長為 ( )
將矩形紙片ABCD按如圖所示的方式折疊,得到菱形AECF.若AB=3,則BC的長為 ( )| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
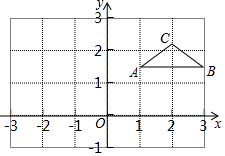 如圖,△ABC在平面直角坐標系內,它的三個頂點的坐標分別為A(1,$\sqrt{2}$),B(3,$\sqrt{2}$),C(2,$\sqrt{5}$),求△ABC的面積.
如圖,△ABC在平面直角坐標系內,它的三個頂點的坐標分別為A(1,$\sqrt{2}$),B(3,$\sqrt{2}$),C(2,$\sqrt{5}$),求△ABC的面積.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com