
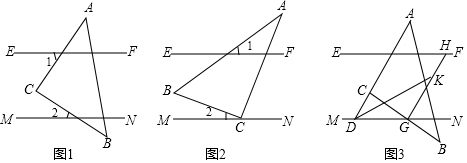
分析 (1)過C作CP∥EF,進而得到EF∥MN∥CP,根據平行線的性質,即可得出∠2的度數;
(2)過B作BQ∥EF,進而得到EF∥MN∥BQ,根據平行線的性質,即可得到∠2的度數;
(3)先根據∠CGN是△CDG的外角,得到∠DCG=∠CGN-∠ADG,再根據GH平分∠CGN,DK平分∠ADN,即可得出∠KGN=$\frac{1}{2}$∠CGN,∠KDG=$\frac{1}{2}$∠ADG,最后根據∠KGN是△KDG的外角,且∠ACB=90°,即可得到∠GKD=∠KGN-∠KDG=$\frac{1}{2}$∠CGN-$\frac{1}{2}$∠ADG=$\frac{1}{2}$∠DCG,根據∠DCG的度數不變,可得∠GKD為定值45°.
解答  解:(1)如圖1,過C作CP∥EF,
解:(1)如圖1,過C作CP∥EF,
∵EF∥MN,
∴EF∥MN∥CP,
∴∠1=∠ACP=60°,
又∵∠ACB=90°,
∴∠BCP=90°-60°=30°,
∵CP∥MN,
∴∠2=∠BCP=30°;
故答案為:30;
(2)如圖2,過B作BQ∥EF,
∵EF∥MN,
∴EF∥MN∥BQ,
∴∠1=∠ABQ,∠2=∠CBQ,
∴∠1+∠2=∠ABC,
又∵∠1=∠ABC-20°,
∴∠1+20°=∠ABC,
∴∠2=20°;
故答案為:20;
(3)∠GKD為定值45°.
理由:如圖3,∵∠CGN是△CDG的外角,
∴∠DCG=∠CGN-∠ADG,
∵GH平分∠CGN,DK平分∠ADN,
∴∠KGN=$\frac{1}{2}$∠CGN,∠KDG=$\frac{1}{2}$∠ADG,
∵∠KGN是△KDG的外角,且∠ACB=90°,
∴∠GKD=∠KGN-∠KDG=$\frac{1}{2}$∠CGN-$\frac{1}{2}$∠ADG=$\frac{1}{2}$(∠CGN-∠ADG)=$\frac{1}{2}$∠DCG=$\frac{1}{2}$×90°=45°,
故∠GKD為定值45°.
點評 本題主要考查了平行線的性質以及三角形外角性質的運用,解題時注意:兩直線平行,內錯角相等.解決第(3)問時,需要運用:三角形的一個外角等于和它不相鄰的兩個內角的和.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
 如圖,在直角坐標系中,點A是反比例函數y1=$\frac{k}{x}$圖象上一點,AB⊥x軸的正半軸于點B,點C是OB的中點,一次函數y2=ax+b的圖象經過A、C兩點,交y軸于點D(0,-2),△AOB的面積為4
如圖,在直角坐標系中,點A是反比例函數y1=$\frac{k}{x}$圖象上一點,AB⊥x軸的正半軸于點B,點C是OB的中點,一次函數y2=ax+b的圖象經過A、C兩點,交y軸于點D(0,-2),△AOB的面積為4查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
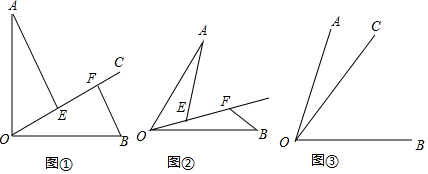
 如圖,四邊形ABCD中,∠ADC的角平分線DE與∠BCD的角平分線CA相交于E點,DE交BC于點F,連結AF,已知∠ACD=32°,∠CDE=58°.
如圖,四邊形ABCD中,∠ADC的角平分線DE與∠BCD的角平分線CA相交于E點,DE交BC于點F,連結AF,已知∠ACD=32°,∠CDE=58°.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com