
分析 先利用坐標軸上點的坐標特征求出直線與x軸和y軸的坐標,則利用三角形面積公式得到Sn=$\frac{1}{n(n+1)}$,再分別計算出S1,S2,S3,S2015,然后利用$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$求它們的和.
解答 解:當x=0時,y=$\frac{\sqrt{2}}{n+1}$,則直線與y軸的交點坐標為(0,$\frac{\sqrt{2}}{n+1}$),
當y=0時,x=$\frac{\sqrt{2}}{n}$,則直線與x軸的交點坐標為($\frac{\sqrt{2}}{n}$,0),
所以Sn=$\frac{1}{2}$•$\frac{\sqrt{2}}{n}$•$\frac{\sqrt{2}}{n+1}$=$\frac{1}{n(n+1)}$,
當n=1時,S1=$\frac{1}{1×2}$,
當n=2時,S2=$\frac{1}{2×3}$,
當n=3時,S3=$\frac{1}{3×4}$,
…
當n=2016時,S2016=$\frac{1}{2016×2017}$,
所以S1+S2+S3+…+S2015=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$=1-$\frac{1}{2017}$=$\frac{2016}{2017}$.
點評 本題考查了一次函數圖象上點的坐標特征:一次函數圖象上點的坐標滿足其解析式,解決此類問題時求出直線與坐標軸的交點坐標.熟練運用$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$是解決此題的關鍵.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:解答題
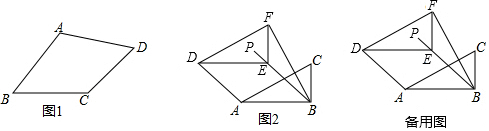
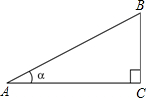 如圖,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα=$\frac{角α的鄰邊}{角α的對邊}$=$\frac{AC}{BC}$,根據上述角的余切定義,解下列問題:
如圖,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα=$\frac{角α的鄰邊}{角α的對邊}$=$\frac{AC}{BC}$,根據上述角的余切定義,解下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
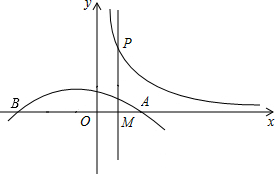 如圖,拋物線L:y=-$\frac{1}{2}$(x-1)(x+3)與x軸從左到右的交點為B,A,過線段OA的中點M作MP⊥x軸,交雙曲線y=$\frac{k}{x}$(k>0,x>0)于點P,且OA•MP=8.
如圖,拋物線L:y=-$\frac{1}{2}$(x-1)(x+3)與x軸從左到右的交點為B,A,過線段OA的中點M作MP⊥x軸,交雙曲線y=$\frac{k}{x}$(k>0,x>0)于點P,且OA•MP=8.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
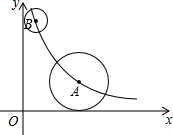 如圖,在平面直角坐標系中,點A、B均在函數y=$\frac{k}{x}$(k>0,x>0)的圖象上,⊙A與x軸相切,⊙B與y軸相切.若點A的坐標為(3,2),且⊙A的半徑是⊙B的半徑的2倍,則點B的坐標為(1,6).
如圖,在平面直角坐標系中,點A、B均在函數y=$\frac{k}{x}$(k>0,x>0)的圖象上,⊙A與x軸相切,⊙B與y軸相切.若點A的坐標為(3,2),且⊙A的半徑是⊙B的半徑的2倍,則點B的坐標為(1,6).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
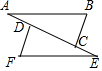 如圖,已知,∠A=∠E,AD=EC,若要△ABC≌△EFD,則可添加下列條件的是( )
如圖,已知,∠A=∠E,AD=EC,若要△ABC≌△EFD,則可添加下列條件的是( )| A. | AB=EF | B. | AC=ED | C. | BC=DF | D. | ∠B=∠BDF |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com