
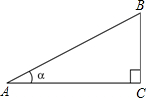
 如圖,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα=$\frac{角α的鄰邊}{角α的對邊}$=$\frac{AC}{BC}$,根據上述角的余切定義,解下列問題:
如圖,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα=$\frac{角α的鄰邊}{角α的對邊}$=$\frac{AC}{BC}$,根據上述角的余切定義,解下列問題:分析 (1)當α=30°時,利用其正切值可求得$\frac{BC}{AC}$的值,根據余切的定義可求得答案;
(2)由正切函數的定義可知$\frac{BC}{AC}$的值,則可求得$\frac{AC}{BC}$的值,可求得ctanA的值;
(3)過點A、B分別作x軸的垂線,垂足分別為C、D,則可證得△OAC∽△BOD,由ctanA=$\frac{\sqrt{3}}{3}$,可求得其相似比,則可求得△BOD的面積,則可求得k的值.
解答 解:
(1)∵tanα=$\frac{BC}{AC}$,
∴tan30°=$\frac{BC}{AC}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{AC}{BC}$=$\sqrt{3}$,
∴ctan30°=$\frac{AC}{BC}$=$\sqrt{3}$,
故答案為:$\sqrt{3}$;
(2)在Rt△ABC中,tanA=$\frac{BC}{AC}$=$\frac{3}{4}$,
∴$\frac{AC}{BC}$=$\frac{4}{3}$,
∴ctanA=$\frac{4}{3}$;
(3)如圖,分別過點A、B作x軸的垂線,垂足分別為C、D,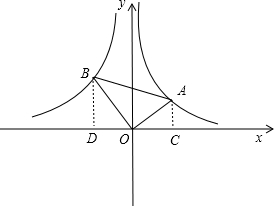
∵A在反比例函數y=$\frac{2}{x}$的圖象上,
∴S△AOC=$\frac{1}{2}$OC•AC=$\frac{1}{2}$×2=1,
∵ctanA=$\frac{\sqrt{3}}{3}$,
∴$\frac{OA}{OB}$=$\frac{\sqrt{3}}{3}$,
∵OA⊥OB,
∴∠AOC+∠BOD=∠BOD+∠OBD=90°,
∴∠AOC=∠OBD,且∠ACO=∠BDO=90°,
∴△OAC∽△BOD,
∴$\frac{{S}_{△OAC}}{{S}_{△BOD}}$=($\frac{OA}{OB}$)2=($\frac{\sqrt{3}}{3}$)2=$\frac{1}{3}$,即$\frac{1}{{S}_{△BOD}}$=$\frac{1}{3}$,
∴S△BOD=3,
∵S△BOD=$\frac{1}{2}$OD•BD=-$\frac{1}{2}$k,
∴-$\frac{1}{2}$k=3,解得k=-6.
點評 本題為反比例函數的綜合應用,涉及三角函數的定義、特別角的三角函數值、相似三角形的判定和性質、反比例函數中k的幾何意義等知識.在(1)、(2)中理角余切值的定義是解題的關鍵,在(3)中求得△BOD的面積是解題的關鍵.本題為新定義型題目,關鍵是理解題目中所給的新定義,難度不大.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案科目:初中數學 來源: 題型:選擇題
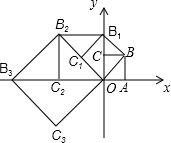 如圖,在平面直角坐標系中有一邊長為1的正方形OABC,邊OA、OC分別在x軸、y軸上,如果以對角線OB為邊作第二個正方形OBB1C1,再以對角線OB1為邊作第三個正方形OB1B2C2,照此規律作下去,則點B2015的坐標為( )
如圖,在平面直角坐標系中有一邊長為1的正方形OABC,邊OA、OC分別在x軸、y軸上,如果以對角線OB為邊作第二個正方形OBB1C1,再以對角線OB1為邊作第三個正方形OB1B2C2,照此規律作下去,則點B2015的坐標為( )| A. | (21008,0) | B. | (21007,-21007) | C. | (21009,21009) | D. | (-21007,21007) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在直角坐標系中,點A是反比例函數y1=$\frac{k}{x}$圖象上一點,AB⊥x軸的正半軸于點B,點C是OB的中點,一次函數y2=ax+b的圖象經過A、C兩點,交y軸于點D(0,-2),△AOB的面積為4
如圖,在直角坐標系中,點A是反比例函數y1=$\frac{k}{x}$圖象上一點,AB⊥x軸的正半軸于點B,點C是OB的中點,一次函數y2=ax+b的圖象經過A、C兩點,交y軸于點D(0,-2),△AOB的面積為4查看答案和解析>>
科目:初中數學 來源: 題型:解答題
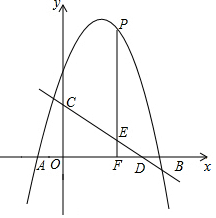 如圖,拋物線y=-x2+4x+5與x軸交于A,B兩點(點A在點B的左側),直線y=$-\frac{3}{4}x+3$與y軸交于點C,與x軸交于點D.P是x軸上方的拋物線上一動點,過點P作PF⊥x軸于點F,交直線CD于點E,設點P的橫坐標為m.
如圖,拋物線y=-x2+4x+5與x軸交于A,B兩點(點A在點B的左側),直線y=$-\frac{3}{4}x+3$與y軸交于點C,與x軸交于點D.P是x軸上方的拋物線上一動點,過點P作PF⊥x軸于點F,交直線CD于點E,設點P的橫坐標為m.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com