
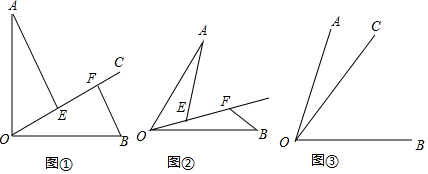
分析 (1)先判斷出∠BOF=∠A,進而得出△AOE≌△OBF,即可得出AE=OF;
(2)同(1)的方法即可得出結論;
(3)①借助(2)的結論AE=OF和圖形即可得出結論;
②同(2)的方法得出AE=OF,在借助圖形即可得出結論.
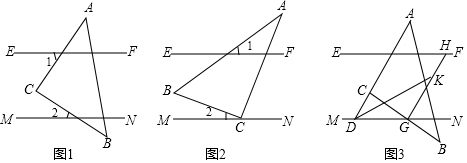
解答 解:(1)∵∠AOB=90°,
∴∠AOC+∠BOF=90°,
∵∠AEO=90°,
∴∠A+∠AOC=90°,
∴∠BOF=∠A,
在△AOE和△OBF中,$\left\{\begin{array}{l}{∠AEO=∠BFO=90°}\\{∠A=∠BOF}\\{AO=BO}\end{array}\right.$,
∴△AOE≌△OBF,
∴AE=OF,
(2)∵∠AOE+∠A+∠AEO=180°,∠AOB+∠AEO=180°,
∴∠AOE+∠A=∠AOB=∠AOE+∠BOF,
∴∠A=∠BOF,
在△AOE和△OBF中,$\left\{\begin{array}{l}{∠AEO=∠BFO}\\{∠A=∠BOF}\\{AO=BO}\end{array}\right.$,
∴△AOE≌△OBF,
∴AE=OF;
(3)①如圖②,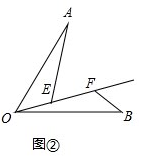
由(2)知AE=OF,
∵OF=OE+EF,
∴AE=OE+EF,
②如圖③,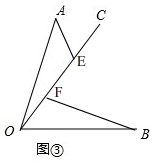
同(2)的方法得,AE=OF,
∵OF=OE-EF,
∴AE=OE-EF.
點評 此題是三角形綜合題,主要考查了等角的余角相等和補角相等,三角形全等的判定和性質,解本題的關鍵是△AOE≌△OBF,用到類比的思想方法解決(2)(3)問,是一道中等難度的中考常考題.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案科目:初中數學 來源: 題型:選擇題
 如圖,點A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分別為D,E,∠DCE=40°,則∠P的度數為( )
如圖,點A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分別為D,E,∠DCE=40°,則∠P的度數為( )| A. | 70° | B. | 60° | C. | 40° | D. | 35° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
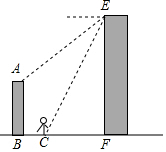 為紀念京漢鐵路工人大罷工而修建的二七紀念塔于去年下半年重新整修,一裝修工在塔EF的頂部處測得對面一棟AB=9米高的樓房頂部A的俯角為45°,測得樓房正前方BC=7米處一站牌底部C點的俯角為60°,請你幫助裝修工人計算塔的高度是多少?($\sqrt{3}$≈1.732,結果保留到1米.)
為紀念京漢鐵路工人大罷工而修建的二七紀念塔于去年下半年重新整修,一裝修工在塔EF的頂部處測得對面一棟AB=9米高的樓房頂部A的俯角為45°,測得樓房正前方BC=7米處一站牌底部C點的俯角為60°,請你幫助裝修工人計算塔的高度是多少?($\sqrt{3}$≈1.732,結果保留到1米.)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
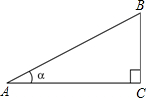 如圖,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα=$\frac{角α的鄰邊}{角α的對邊}$=$\frac{AC}{BC}$,根據上述角的余切定義,解下列問題:
如圖,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα=$\frac{角α的鄰邊}{角α的對邊}$=$\frac{AC}{BC}$,根據上述角的余切定義,解下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
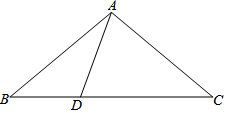 在△ABC中,已知D為直線BC上一點,若∠ABC=x°,∠BAD=y°.
在△ABC中,已知D為直線BC上一點,若∠ABC=x°,∠BAD=y°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
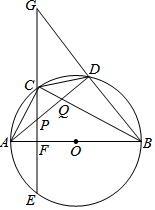 已知:如圖,△ABC內接于⊙O,AB為直徑,弦CE⊥AB于F,D是弧BC上的一點,CD=AE,連結BD并延長交EC的延長線于點G,連結AD,分別交CE、BC于點P、Q.
已知:如圖,△ABC內接于⊙O,AB為直徑,弦CE⊥AB于F,D是弧BC上的一點,CD=AE,連結BD并延長交EC的延長線于點G,連結AD,分別交CE、BC于點P、Q.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
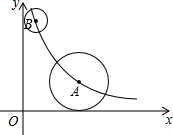 如圖,在平面直角坐標系中,點A、B均在函數y=$\frac{k}{x}$(k>0,x>0)的圖象上,⊙A與x軸相切,⊙B與y軸相切.若點A的坐標為(3,2),且⊙A的半徑是⊙B的半徑的2倍,則點B的坐標為(1,6).
如圖,在平面直角坐標系中,點A、B均在函數y=$\frac{k}{x}$(k>0,x>0)的圖象上,⊙A與x軸相切,⊙B與y軸相切.若點A的坐標為(3,2),且⊙A的半徑是⊙B的半徑的2倍,則點B的坐標為(1,6).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com