
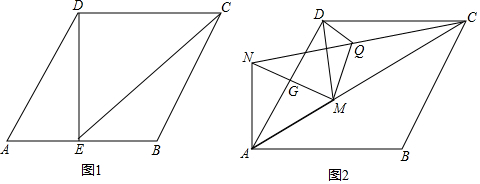
分析 (1)如圖1,連接對角線BD,先證明△ABD是等邊三角形,根據E是AB的中點,由等腰三角形三線合一得:DE⊥AB,利用勾股定理依次求DE和EC的長;
(2)如圖2,作輔助線,構建全等三角形,先證明△ADH是等邊三角形,再由△AMN是等邊三角形,得條件證明△ANH≌△AMD(SAS),則HN=DM,根據DQ是△CHN的中位線,得HN=2DQ,由等量代換可得結論.
解答 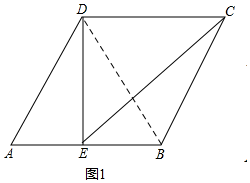 解:(1)如圖1,連接BD,則BD平分∠ABC,
解:(1)如圖1,連接BD,則BD平分∠ABC,
∵四邊形ABCD是菱形,
∴AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=60°,
∴∠ABC=120°,
∴∠ABD=$\frac{1}{2}$∠ABC=60°,
∴△ABD是等邊三角形,
∴BD=AD=4,
∵E是AB的中點,
∴DE⊥AB,
由勾股定理得:DE=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵DC∥AB,
∴∠EDC=∠DEA=90°,
在Rt△DEC中,DC=4,
EC=$\sqrt{D{C}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{3})^{2}}$=2$\sqrt{7}$;
(2)如圖2,延長CD至H,使CD=DH,連接NH、AH,
∵AD=CD,
∴AD=DH,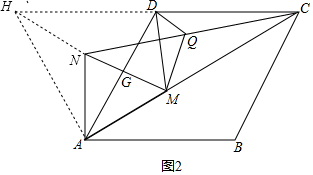
∵CD∥AB,
∴∠HDA=∠BAD=60°,
∴△ADH是等邊三角形,
∴AH=AD,∠HAD=60°,
∵△AMN是等邊三角形,
∴AM=AN,∠NAM=60°,
∴∠HAN+∠NAG=∠NAG+∠DAM,
∴∠HAN=∠DAM,
在△ANH和△AMD中,
∵$\left\{\begin{array}{l}{AH=AD}\\{∠HAN=∠DAM}\\{AN=AM}\end{array}\right.$,
∴△ANH≌△AMD(SAS),
∴HN=DM,
∵D是CH的中點,Q是NC的中點,
∴DQ是△CHN的中位線,
∴HN=2DQ,
∴DM=2DQ.
點評 本題考查了菱形的性質、三角形的中位線、三角形全等的性質和判定、等邊三角形的性質和判定,本題證明△ANH≌△AMD是關鍵,并與三角形中位線相結合,解決問題;第二問有難度,注意輔助線的構建.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
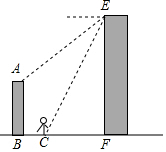 為紀念京漢鐵路工人大罷工而修建的二七紀念塔于去年下半年重新整修,一裝修工在塔EF的頂部處測得對面一棟AB=9米高的樓房頂部A的俯角為45°,測得樓房正前方BC=7米處一站牌底部C點的俯角為60°,請你幫助裝修工人計算塔的高度是多少?($\sqrt{3}$≈1.732,結果保留到1米.)
為紀念京漢鐵路工人大罷工而修建的二七紀念塔于去年下半年重新整修,一裝修工在塔EF的頂部處測得對面一棟AB=9米高的樓房頂部A的俯角為45°,測得樓房正前方BC=7米處一站牌底部C點的俯角為60°,請你幫助裝修工人計算塔的高度是多少?($\sqrt{3}$≈1.732,結果保留到1米.)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
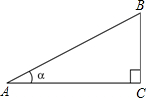 如圖,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα=$\frac{角α的鄰邊}{角α的對邊}$=$\frac{AC}{BC}$,根據上述角的余切定義,解下列問題:
如圖,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα=$\frac{角α的鄰邊}{角α的對邊}$=$\frac{AC}{BC}$,根據上述角的余切定義,解下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
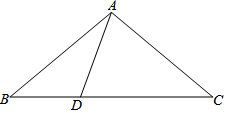 在△ABC中,已知D為直線BC上一點,若∠ABC=x°,∠BAD=y°.
在△ABC中,已知D為直線BC上一點,若∠ABC=x°,∠BAD=y°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
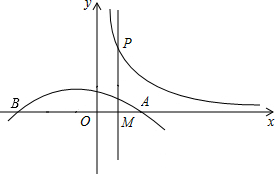 如圖,拋物線L:y=-$\frac{1}{2}$(x-1)(x+3)與x軸從左到右的交點為B,A,過線段OA的中點M作MP⊥x軸,交雙曲線y=$\frac{k}{x}$(k>0,x>0)于點P,且OA•MP=8.
如圖,拋物線L:y=-$\frac{1}{2}$(x-1)(x+3)與x軸從左到右的交點為B,A,過線段OA的中點M作MP⊥x軸,交雙曲線y=$\frac{k}{x}$(k>0,x>0)于點P,且OA•MP=8.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com