
 如圖,AB為⊙O的直徑,$\widehat{CB}$=$\widehat{CD}$,CO的延長線交⊙O于點E,BA,ED的延長線交于點F.
如圖,AB為⊙O的直徑,$\widehat{CB}$=$\widehat{CD}$,CO的延長線交⊙O于點E,BA,ED的延長線交于點F.分析 (1)根據$\widehat{CB}$=$\widehat{CD}$,$\widehat{CB}+\widehat{BE}=\widehat{CD}+\widehat{DE}$,可以證明結論成立;
(2)要求$\frac{AE}{BE}$的值,根據三角形相似和勾股定理可以求得$\frac{AE}{BE}$的值,本題得以解決.
解答 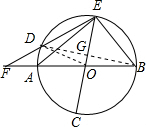 (1)證明:∵$\widehat{CB}$=$\widehat{CD}$,$\widehat{CB}+\widehat{BE}=\widehat{CD}+\widehat{DE}$,
(1)證明:∵$\widehat{CB}$=$\widehat{CD}$,$\widehat{CB}+\widehat{BE}=\widehat{CD}+\widehat{DE}$,
∴$\widehat{BE}=\widehat{DE}$,
∵$\widehat{AC}=\widehat{BE}$,
∴$\widehat{AC}$=$\widehat{DE}$;
(2)連接BD,
∵$\widehat{BE}=\widehat{DE}$,
∴BD⊥EC,
∵DEG∽△AEB,
∴$\frac{DG}{DE}=\frac{AE}{AB}$,
∴$\frac{\frac{1}{2}BD}{DE}=\frac{AE}{AB}$,
∴$\frac{AE}{BD}=\frac{AB}{2DE}$,
∵△FAE∽△FDB,
∴$\frac{AF}{DF}=\frac{AE}{DB}=\frac{2}{3}$,
∴$\frac{AB}{2DE}=\frac{2}{3}$,
∴$\frac{AB}{DE}=\frac{4}{3}$,
∴$\frac{AB}{BE}=\frac{4}{3}$,
設AB=4x,BE=3x,
∴AE=$\sqrt{7}$x,
∴$\frac{AE}{BE}=\frac{\sqrt{7}}{3}$.
點評 本題考查三角形相似性質和判定、圓周角定理、勾股定理,解答此類問題的關鍵是明確題意,找出所求問題需要的條件,利用三角形的相似解答.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,AB=AC,以AB為直徑的O交BC于點D,過點D作EF⊥AC于點E,交AB的延長線于點F.
如圖,在△ABC中,AB=AC,以AB為直徑的O交BC于點D,過點D作EF⊥AC于點E,交AB的延長線于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在梯形ABCD中,AB∥CD,AC、BD交于點E,AD、BC的延長線交于點H,過點E作FG∥AB交AD于點F,交BC于點G,求證:AG、BF、EH三線共點.
在梯形ABCD中,AB∥CD,AC、BD交于點E,AD、BC的延長線交于點H,過點E作FG∥AB交AD于點F,交BC于點G,求證:AG、BF、EH三線共點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
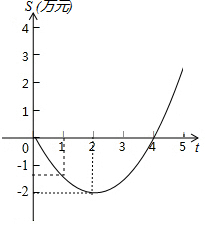 某電腦公司開發出一種軟件,從研發到年初上市后,經歷了從虧損到盈利的過程,如圖中的圖象是拋物線的一段,它刻畫了該軟件上市以來累積利潤S(萬元)與銷售時間t(月)之間的函數關系(即前t個月的利潤總和S與t之間的函數關系),根據圖象提供的信息,解答下列問題:
某電腦公司開發出一種軟件,從研發到年初上市后,經歷了從虧損到盈利的過程,如圖中的圖象是拋物線的一段,它刻畫了該軟件上市以來累積利潤S(萬元)與銷售時間t(月)之間的函數關系(即前t個月的利潤總和S與t之間的函數關系),根據圖象提供的信息,解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 已知,直線y=-$\sqrt{3}$x+$\sqrt{3}$與x軸、y軸分別交于點A、B,以線段AB為直角邊在第一象限內作等腰三角形Rt△ABC,∠BAC=90°,且點P(1,a)為坐標系中一個動點.要使得△ABC和△ABP的面積相等,則實數a的值( )
已知,直線y=-$\sqrt{3}$x+$\sqrt{3}$與x軸、y軸分別交于點A、B,以線段AB為直角邊在第一象限內作等腰三角形Rt△ABC,∠BAC=90°,且點P(1,a)為坐標系中一個動點.要使得△ABC和△ABP的面積相等,則實數a的值( )| A. | a=4 | B. | a=±4 | C. | a=-3 | D. | a=±3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com