
分析 把$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$化為$\sqrt{(x-0)^{2}+(0-2)^{2}}$+$\sqrt{(3-x)^{2}+(0-4)^{2}}$根據兩點間的距離得到$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$的最小值=3$\sqrt{5}$,解方程即可得到結論.
解答 解;求代數式$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$的最小值,即求$\sqrt{{x}^{2}+4}$+$\sqrt{(3-x)^{2}+16}$的最小值,
∴$\sqrt{(x-0)^{2}+(0-2)^{2}}$+$\sqrt{(3-x)^{2}+(0-4)^{2}}$的最小值,
實際上就是求x軸上一點到(0,-2)以及(3,4)兩點的和的最小值,
而兩點間的距離是線段最短,所以,點到(0,-2)到點(3,4)的距離即為所求,
即$\sqrt{{3}^{2}+(4+2)^{2}}$=3$\sqrt{5}$,
∴$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$的最小值=3$\sqrt{5}$,
解$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$=3$\sqrt{5}$得x=-1,
∴當x為-1時,$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$取得最小值.
點評 本題考查了軸對稱-最短路線問題,解方程,正確的理解題意是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
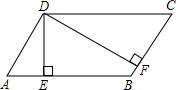 如圖,在平行四邊形ABCD中,DE⊥AB,DF⊥BC,若DE+DF=10,平行四邊形ABCD的邊長AB=9,BC=6,求平行四邊形ABCD的面積.
如圖,在平行四邊形ABCD中,DE⊥AB,DF⊥BC,若DE+DF=10,平行四邊形ABCD的邊長AB=9,BC=6,求平行四邊形ABCD的面積.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
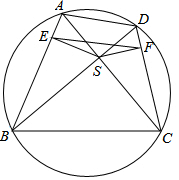 如圖所示,圓的內接四邊形ABCD的兩條對角線AC、BD的交點為S,S在邊AB、CD上的投影分別為E、F.證明EF的中垂線平分線段AD、BC.
如圖所示,圓的內接四邊形ABCD的兩條對角線AC、BD的交點為S,S在邊AB、CD上的投影分別為E、F.證明EF的中垂線平分線段AD、BC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,點P從點A出發,沿AB方向以每秒$\sqrt{2}$cm的速度向終點B運動;同時,動點Q從點B出發,沿BC方向以每秒1cm的速度向終點C運動,當△PQC為以QC為底邊的等腰三角形的時候,時間t的值為多少?
如圖,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,點P從點A出發,沿AB方向以每秒$\sqrt{2}$cm的速度向終點B運動;同時,動點Q從點B出發,沿BC方向以每秒1cm的速度向終點C運動,當△PQC為以QC為底邊的等腰三角形的時候,時間t的值為多少?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,兩根旗桿AC與BD相距12m,某人從B點沿AB走向A,一定時間后他到達點M,此時他仰望旗桿的頂點C和D,兩次視線夾角為90°,且CM=DM.已知旗桿AC的高為3m,該人的運動速度為0.5m/s,求這個人走了多長時間?
如圖,兩根旗桿AC與BD相距12m,某人從B點沿AB走向A,一定時間后他到達點M,此時他仰望旗桿的頂點C和D,兩次視線夾角為90°,且CM=DM.已知旗桿AC的高為3m,該人的運動速度為0.5m/s,求這個人走了多長時間?查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 大于1.55米且小于1.65米 | B. | 不小于1.55米且小于1.65米 | ||
| C. | 大于1.55米且不大于1.65米 | D. | 不小于1.55米且不大于1.65米 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2 | B. | 8 | C. | 2或8 | D. | 8或16 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 開口向下 | B. | 頂點坐標是(-1,2) | C. | 對稱軸是x=1 | D. | 與x軸有兩個交點 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com