
| A. | 2 | B. | 8 | C. | 2或8 | D. | 8或16 |
分析 分兩種情況:①若BC為等腰三角形的腰,即方程x2-5mx+4m2=0有一個根為8,將x=8代入方程求得m的值,再將m的值代回方程求得x的值,根據(jù)三角形三邊之間的關(guān)系判斷是否能構(gòu)成三角形;②若BC為等腰三角形的底邊,則方程x2-5mx+4m2=0有兩個相等的實(shí)數(shù)根,根據(jù)判別式為0求得m的值,再判斷即可得.
解答 解:根據(jù)題意,若BC為等腰三角形的腰,則方程x2-5mx+4m2=0有一個根為8,
將x=8代入得:64-40m+4m2=0,即m2-10m+16=0,
解得:m=2或m=8,
當(dāng)m=2時,方程為x2-10x+16=0,解得:x=2或x=8,符合題意;
當(dāng)m=8時,方程為x2-40x+256=0,解得:x=32或x=8,
此時8+8<32,不能構(gòu)成三角形,舍去;
若BC為等腰三角形的底邊,則方程x2-5mx+4m2=0有兩個相等的實(shí)數(shù)根,
∴△=25m2-16m2=0,
解得:m=0,
此時方程為x2=0,得x=0,不符合題意,舍去;
綜上m的值為2,
故選:A.
點(diǎn)評 本題主要考查根的判別式、方程的解的定義、等腰三角形的性質(zhì)及三角形三邊之間的關(guān)系,根據(jù)等腰三角形的性質(zhì)分類討論是解題的關(guān)鍵.


 培優(yōu)好卷單元加期末卷系列答案
培優(yōu)好卷單元加期末卷系列答案 一線名師權(quán)威作業(yè)本系列答案
一線名師權(quán)威作業(yè)本系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1004<a<1005 | B. | 1004≤a<1005 | ||
| C. | 1004<a<1005或-1005≤a<-1004 | D. | 1004≤a<1005或-1005<a≤-1004 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
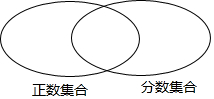 把下列各數(shù)填在相應(yīng)的圓圈集合內(nèi):
把下列各數(shù)填在相應(yīng)的圓圈集合內(nèi):查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
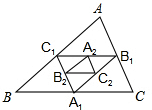 如圖,在△ABC中,A1、B1、C1分別是BC、CA、AB的中點(diǎn),A2、B2、C2分別是B1C1、C1A1、A1B1的中點(diǎn),…,An、Bn、Cn分別是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中點(diǎn),假設(shè)△ABC的周長為a,則△A1B1C1的周長為$\frac{1}{2}$a,△A2B2C2的周長為$\frac{1}{4}$a,…,△AnBnCn的周長為$\frac{1}{{2}^{n}}$a.
如圖,在△ABC中,A1、B1、C1分別是BC、CA、AB的中點(diǎn),A2、B2、C2分別是B1C1、C1A1、A1B1的中點(diǎn),…,An、Bn、Cn分別是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中點(diǎn),假設(shè)△ABC的周長為a,則△A1B1C1的周長為$\frac{1}{2}$a,△A2B2C2的周長為$\frac{1}{4}$a,…,△AnBnCn的周長為$\frac{1}{{2}^{n}}$a.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 正整數(shù)和正分?jǐn)?shù)統(tǒng)稱正有理數(shù) | B. | 兩個無理數(shù)相乘的結(jié)果可能等于零 | ||
| C. | 正整數(shù),0,負(fù)整數(shù)統(tǒng)稱為整數(shù) | D. | 3.1415926是小數(shù),也是分?jǐn)?shù) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
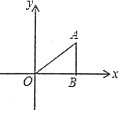 如圖.在△ABO中,AB丄OB,OB=$\sqrt{3}$,AB=1,將△ABO繞O點(diǎn)逆時計(jì)旋轉(zhuǎn)90°后得到△A1B1O,則點(diǎn)A1的坐標(biāo)為( )
如圖.在△ABO中,AB丄OB,OB=$\sqrt{3}$,AB=1,將△ABO繞O點(diǎn)逆時計(jì)旋轉(zhuǎn)90°后得到△A1B1O,則點(diǎn)A1的坐標(biāo)為( )| A. | (-1,$\sqrt{3}$) | B. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | C. | (-1,-$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$)或(-$\sqrt{3}$,-1) |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com