
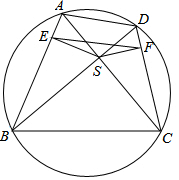
 如圖所示,圓的內(nèi)接四邊形ABCD的兩條對(duì)角線AC、BD的交點(diǎn)為S,S在邊AB、CD上的投影分別為E、F.證明EF的中垂線平分線段AD、BC.
如圖所示,圓的內(nèi)接四邊形ABCD的兩條對(duì)角線AC、BD的交點(diǎn)為S,S在邊AB、CD上的投影分別為E、F.證明EF的中垂線平分線段AD、BC. 分析 先判斷出△BES∽△CFS得出BS•FS=CS•ES,∠CSE=∠BSF,即可得出BS•FS•cos∠BSF=CS•ES•cos∠CSE,再根據(jù)余弦定理得,BS2+FS2-BF2=CS2+ES2-EC2,即:BS2-ES2+EC2=CS2-FS2+BF2,再根據(jù)勾股定理得出結(jié)論結(jié)合前面的式子得出BE2+EC2=CF2+BF2①,最后用勾股定理和中點(diǎn)即可得出EB2+EC2=2(EM2+BM2)④,同樣的辦法得出
FB2+FC2=2(FM2+BM2)⑤,結(jié)合①④⑤即可判斷出EF的中垂線平分線段BC,即可得出結(jié)論.
解答 解:如圖, 連接BF,CE,
連接BF,CE,
∵S在邊AB、CD上的投影分別為E、F,
∴∠BES=∠CFS=90°,
∵∠EBS=∠FCS,
∴△BES∽△CFS,
∴∠BSE=∠CSF,
∴∠CSE=∠BSF,
∵△BES∽△CFS,
∴∠$\frac{BS}{CS}=\frac{ES}{FS}$,
∴BS•FS=CS•ES,
∴BS•FS•cos∠BSF=CS•ES•cos∠CSE,
根據(jù)余弦定理得,BS2+FS2-BF2=CS2+ES2-EC2,
∴BS2-ES2+EC2=CS2-FS2+BF2,
在Rt△BES中,BS2-ES2=BE2,
在Rt△CFS中,CS2-FS2=CF2,
∴BE2+EC2=CF2+BF2①,
取BC的中點(diǎn)M,連接EM,F(xiàn)M
∴BM=CM,
作EH⊥BC于H,
∴BH=BM-HM,
在Rt△EMH中,EM2=EH2+MH2,
在Rt△EBH中,EB2=EH2+BH2=EH2+(BM-HM)2=EH2+BM2+HM2-2BM•HM+HM2,
∴EB2=EM2+BM2-2BM•HM=EM2+CM2-2CM•HM②,
同理:EC2=EM2+CM2+2CM•HM③,
②+③得,EB2+EC2=2EM2+2CM2=2(EM2+CM2)=2(EM2+BM2)④,
同理:FB2+FC2=2(FM2+BM2)⑤,
由①④⑤得,2(EM2+BM2)=2(FM2+BM2),
∴EM=FM,
∴△EMF是等腰三角形,
∵點(diǎn)M是BC的中點(diǎn),
∴點(diǎn)M是EF的垂直平分線上,
∴EF的中垂線平分線段BC.
同理:EF的中垂線平分線段AD.
即:EF的中垂線平分線段AD、BC.
點(diǎn)評(píng) 此題是圓的綜合題.主要考查了相似三角形的判定和性質(zhì),余弦定理,勾股定理,等腰三角形的判定和性質(zhì),解本題的關(guān)鍵是EB2+EC2=2(EM2+BM2)和FB2+FC2=2(FM2+BM2),也是解本題的難點(diǎn),是一道難度比較大的競(jìng)賽題.


 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達(dá)標(biāo)測(cè)試卷闖關(guān)100分系列答案
課程達(dá)標(biāo)測(cè)試卷闖關(guān)100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關(guān)100分系列答案
全能闖關(guān)100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1004<a<1005 | B. | 1004≤a<1005 | ||
| C. | 1004<a<1005或-1005≤a<-1004 | D. | 1004≤a<1005或-1005<a≤-1004 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 恢復(fù)原價(jià) | B. | 降價(jià)4% | C. | 提價(jià)4% | D. | 以上都不對(duì) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,在長(zhǎng)和寬分別為m,n的長(zhǎng)方形鐵皮的四個(gè)角都剪去一個(gè)邊長(zhǎng)為x的正方形(2x<n<m),折疊后,做成一無(wú)蓋的盒子,則這個(gè)長(zhǎng)方體盒子的表面積是mn-4x2.
如圖,在長(zhǎng)和寬分別為m,n的長(zhǎng)方形鐵皮的四個(gè)角都剪去一個(gè)邊長(zhǎng)為x的正方形(2x<n<m),折疊后,做成一無(wú)蓋的盒子,則這個(gè)長(zhǎng)方體盒子的表面積是mn-4x2.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
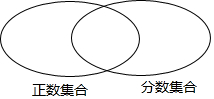 把下列各數(shù)填在相應(yīng)的圓圈集合內(nèi):
把下列各數(shù)填在相應(yīng)的圓圈集合內(nèi):查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 正整數(shù)和正分?jǐn)?shù)統(tǒng)稱正有理數(shù) | B. | 兩個(gè)無(wú)理數(shù)相乘的結(jié)果可能等于零 | ||
| C. | 正整數(shù),0,負(fù)整數(shù)統(tǒng)稱為整數(shù) | D. | 3.1415926是小數(shù),也是分?jǐn)?shù) |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com