
 如圖,兩根旗桿AC與BD相距12m,某人從B點沿AB走向A,一定時間后他到達點M,此時他仰望旗桿的頂點C和D,兩次視線夾角為90°,且CM=DM.已知旗桿AC的高為3m,該人的運動速度為0.5m/s,求這個人走了多長時間?
如圖,兩根旗桿AC與BD相距12m,某人從B點沿AB走向A,一定時間后他到達點M,此時他仰望旗桿的頂點C和D,兩次視線夾角為90°,且CM=DM.已知旗桿AC的高為3m,該人的運動速度為0.5m/s,求這個人走了多長時間? 分析 根據題意證明∠ACM=∠DMB,利用AAS證明△ACM≌△BMD,根據全等三角形的性質得到AC=BM=3m,計算即可.
解答 解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°,
∴∠CMA+∠ACM=90°,
∴∠ACM=∠DMB,
在△ACM和△BMD中,
$\left\{\begin{array}{l}{∠A=∠B}\\{∠AMC=∠DMB}\\{CM=DM}\end{array}\right.$,
∴△ACM≌△BMD(AAS),
∴AC=BM=3m,
∴他到達點M時,運動時間為3÷0.5=6(s),
答:這個人從B點到M點運動了6s.
點評 本題考查的是全等三角形的應用,掌握全等三角形的判定定理和性質定理是解題的關鍵.


科目:初中數學 來源: 題型:填空題
 如圖,在長和寬分別為m,n的長方形鐵皮的四個角都剪去一個邊長為x的正方形(2x<n<m),折疊后,做成一無蓋的盒子,則這個長方體盒子的表面積是mn-4x2.
如圖,在長和寬分別為m,n的長方形鐵皮的四個角都剪去一個邊長為x的正方形(2x<n<m),折疊后,做成一無蓋的盒子,則這個長方體盒子的表面積是mn-4x2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
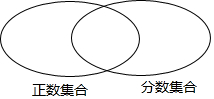 把下列各數填在相應的圓圈集合內:
把下列各數填在相應的圓圈集合內:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 由5x=4x+1可得4x-5x=1 | B. | 由3(x-1)-2(2x-3)=1可得3x-3-4x-6=1 | ||
| C. | 由$\frac{x+2}{4}$-1=$\frac{2x-3}{6}$可得3(x+2)-1=2(2x-3) | D. | 由$\frac{1}{2}$x=$\frac{1}{4}$可得x=$\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com