
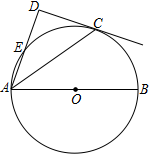
 如圖,點C在以AB為直徑的⊙O上,AC平分∠DAB,AD與過點C的直線垂直,垂足為點D,AD交⊙O于點E.
如圖,點C在以AB為直徑的⊙O上,AC平分∠DAB,AD與過點C的直線垂直,垂足為點D,AD交⊙O于點E.分析 (1)如圖1中,連接OC.只要證明AD∥OC,由AD⊥CD,即可推出OC⊥CD.
(2)如圖2中,連接BE、BC、OC,BE交AC于F交OC于H.由△CDE∽△AEF,推出$\frac{DE}{EF}$=$\frac{DC}{AE}$=$\frac{EC}{AF}$=2,設AE=a,EF=b,則CD=2a,DE=CH=2b,FH=2a-b,由AE∥CH,推出$\frac{AE}{CH}$=$\frac{EF}{FH}$,可得$\frac{a}{2b}$=$\frac{b}{2a-b}$,求出a與b的關系,在Rt△AEF中,求出CF,AF=$\sqrt{A{E}^{2}+E{F}^{2}}$,由此即可解決問題.
解答 (1)證明:如圖1中,連接OC.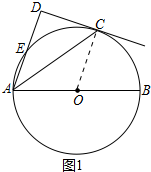
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠DAC=∠CAB=∠ACO,
∴AD∥OC,
∵AD⊥CD,
∴OC⊥DC,
∴CD是⊙O的切線.
(2)解:如圖2中,連接BE、BC、OC,BE交AC于F交OC于H.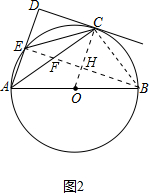
∵AB是直徑,
∴∠AEB=∠DEH=∠D=∠DCH=90°,
∴四邊形DEHC是矩形,
∴∠EHC=90°即OC⊥EB,
∴DC=EH=HB,DE=HC,
∵∠DCE=∠DAC,∠D=∠AEF=90°,
∴△CDE∽△AEF,
∴$\frac{DE}{EF}$=$\frac{DC}{AE}$=$\frac{EC}{AF}$=2,設AE=a,EF=b,則CD=2a,DE=CH=2b,FH=2a-b,
∵AE∥CH,
∴$\frac{AE}{CH}$=$\frac{EF}{FH}$,
∴$\frac{a}{2b}$=$\frac{b}{2a-b}$,
∴2a2-ab-2b2=0,
∴a=$\frac{1+\sqrt{17}}{4}$b或$\frac{1-\sqrt{17}}{4}$b(舍棄),
在Rt△AEF中,AF=$\sqrt{A{E}^{2}+E{F}^{2}}$=$\frac{\sqrt{34+2\sqrt{34}}}{4}$b,
∴cos∠CAD=$\frac{AE}{AF}$=$\frac{\frac{1+\sqrt{17}}{4}b}{\frac{\sqrt{34+2\sqrt{34}}}{4}b}$=$\frac{1+\sqrt{17}}{\sqrt{34+2\sqrt{34}}}$.
點評 本題考查了切線的性質,平行線的性質和判定,勾股定理,圓周角定理,圓心角、弧、弦之間的關系的應用,解此題的關鍵是學會利用參數,構建方程解決問題,題目比較難,有一定的難度.


科目:初中數學 來源: 題型:填空題
 在△ABC中,點D,E分別在AB,AC上,且CD與BE相交于點F,已知△BDF的面積為6,△BCF的面積為9,△CEF的面積為6,則四邊形ADFE的面積為24.
在△ABC中,點D,E分別在AB,AC上,且CD與BE相交于點F,已知△BDF的面積為6,△BCF的面積為9,△CEF的面積為6,則四邊形ADFE的面積為24.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com