
分析 (1)根據多項式除以單項式可以解答本題;
(2)根據完全平方公式和平方差公式可以解答本題;
(3)根據積的乘方、單項式乘單項式和整式的加法可以解答本題;
(4)根據單項式乘多項式和整式的加減法可以解答本題.
解答 解:(1)(4x3-2x2-3x)÷(-3x)
=(4x3-2x2-3x)×($-\frac{1}{3x}$)
=$-\frac{4{x}^{2}}{3}+\frac{2x}{3}+1$;
(2)(2x-y)2-4(y-x)(-x-y)
=4x2-4xy+y2+4y2-4x2
=5y2-4xy;
(3)(2x3y)2•(-2xy)+(-2x3y)3÷(2x2)
=$(4{x}^{6}{y}^{2})•(-2xy)+(-8{x}^{9}{y}^{3})×\frac{1}{2{x}^{2}}$
=-8x7y3-4x7y3
=-12x7y3;
(4)2x(3x+5)-(2x+3)(3x-4)=2(3x+4)
去括號,得
6x2+10x-6x2-x+12=6x+8,
移項及合并同類項,得
3x=-4,
系數化為1,得
x=-$\frac{4}{3}$.
點評 本題考查整式的混合運算,解答本題的關鍵是明確整式的混合運算的計算方法.


科目:初中數學 來源: 題型:填空題
 二次函數y=$\frac{2}{3}$x2的函數圖象如圖,點A0位于坐標原點,點A1,A2,A3…A10 在y軸的正半軸上,點B1,B2,B3…B10在二次函數y=$\frac{2}{3}$x2位于第一象限的圖象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都為等邊三角形,則△A9B10A10的邊長為10.
二次函數y=$\frac{2}{3}$x2的函數圖象如圖,點A0位于坐標原點,點A1,A2,A3…A10 在y軸的正半軸上,點B1,B2,B3…B10在二次函數y=$\frac{2}{3}$x2位于第一象限的圖象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都為等邊三角形,則△A9B10A10的邊長為10.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
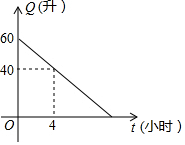 汽車油箱中的余油量Q(升)是它行駛的時間t(小時)的一次函數,某天該汽車外出時,油箱中余油量與行駛時間的變化關系如圖所示,當油箱中余油20升時,該汽車行駛了8小時.
汽車油箱中的余油量Q(升)是它行駛的時間t(小時)的一次函數,某天該汽車外出時,油箱中余油量與行駛時間的變化關系如圖所示,當油箱中余油20升時,該汽車行駛了8小時.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
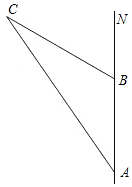 某輪船上午8時從A島出發,以20海里/小時的速度向正北方向航行,如圖,上午10時到達B島,此時得到消息,在C島周圍15海里內有暗礁,經測量得∠NAC=15°,∠NBC=30°,問該輪船繼續向北航行有無觸礁危險?
某輪船上午8時從A島出發,以20海里/小時的速度向正北方向航行,如圖,上午10時到達B島,此時得到消息,在C島周圍15海里內有暗礁,經測量得∠NAC=15°,∠NBC=30°,問該輪船繼續向北航行有無觸礁危險?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 校車安全是近幾年社會關注的重大問題,安全隱患主要是超速和超載.某中學數學活動小組設計了如圖檢測公路上行駛的校車速度的實驗:先在公路旁邊選取一點C,再在筆直的車道l上確定點D,使CD與l垂直,測得CD的長等于30米,在l上點D的同側取點A、B,使∠CAD=30°,∠CBD=45°.
校車安全是近幾年社會關注的重大問題,安全隱患主要是超速和超載.某中學數學活動小組設計了如圖檢測公路上行駛的校車速度的實驗:先在公路旁邊選取一點C,再在筆直的車道l上確定點D,使CD與l垂直,測得CD的長等于30米,在l上點D的同側取點A、B,使∠CAD=30°,∠CBD=45°.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,有一顆棋子放在圖中的1號位置上,現按順時針方向,第一次跳一步到2號位置上第二次跳兩步跳到4號位置上,第三次跳三步又跳到了1號位置上,第四次跳四步…一直進行下去,那么第2017次跳2017步就跳到了2號位置上.
如圖,有一顆棋子放在圖中的1號位置上,現按順時針方向,第一次跳一步到2號位置上第二次跳兩步跳到4號位置上,第三次跳三步又跳到了1號位置上,第四次跳四步…一直進行下去,那么第2017次跳2017步就跳到了2號位置上.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\left\{\begin{array}{l}x>3\\ x>2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x>3\\ x<2\end{array}\right.$ | C. | $\left\{\begin{array}{l}x<3\\ x>2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x<3\\ x<2\end{array}\right.$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
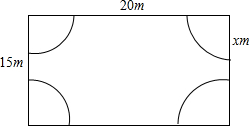 如圖所示,某小區計劃在一塊長20米,寬15米的矩形荒地上建造一個花園,使得花園所占面積為荒地面積的一半,其中花園每個角上的扇形都相同,則每個扇形的半徑x是多少?(精確到0.1)
如圖所示,某小區計劃在一塊長20米,寬15米的矩形荒地上建造一個花園,使得花園所占面積為荒地面積的一半,其中花園每個角上的扇形都相同,則每個扇形的半徑x是多少?(精確到0.1)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
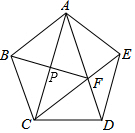 如圖,正五邊形ABCDE中,連接AC、AD、CE,CE交AD于點F,連接BF,BF與AC交于點P.
如圖,正五邊形ABCDE中,連接AC、AD、CE,CE交AD于點F,連接BF,BF與AC交于點P.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com