
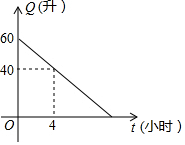
 汽車油箱中的余油量Q(升)是它行駛的時間t(小時)的一次函數,某天該汽車外出時,油箱中余油量與行駛時間的變化關系如圖所示,當油箱中余油20升時,該汽車行駛了8小時.
汽車油箱中的余油量Q(升)是它行駛的時間t(小時)的一次函數,某天該汽車外出時,油箱中余油量與行駛時間的變化關系如圖所示,當油箱中余油20升時,該汽車行駛了8小時. 分析 設一次函數的表達式為Q=kt+b(k≠0),然后利用待定系數法求一次函數解析式,把余油量代入函數解析式求出時間t即可.
解答 解:設一次函數的表達式為Q=kt+b(k≠0)
由圖象可知,函數圖象過(0,60)和(4,40)兩點,
∴$\left\{\begin{array}{l}{b=60}\\{4k+b=40}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-5}\\{b=60}\end{array}\right.$,
∴Q=-5t+60;
當Q=20時,-5t+60=20,
解得t=8,
∴當油箱中余油20升時,該汽車行駛了8小時.
故答案為8.
點評 此題考查了一次函數的應用,已知函數值求自變量的方法,利用待定系數法求出一次函數解析式是解題的關鍵,也是本題的難點


科目:初中數學 來源: 題型:解答題
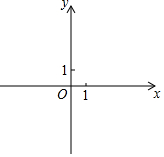 設點Q到圖形W上每一個點的距離的最小值稱為點Q到圖形W的距離.例如正方形ABCD滿足A(1,0),B(2,0),C(2,1),D(1,1),那么點O(0,0)到正方形ABCD的距離為1.
設點Q到圖形W上每一個點的距離的最小值稱為點Q到圖形W的距離.例如正方形ABCD滿足A(1,0),B(2,0),C(2,1),D(1,1),那么點O(0,0)到正方形ABCD的距離為1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
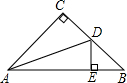 如圖,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于點D,DE⊥AB交AB于點E,AB=4$\sqrt{2}$cm,求△BDE的周長.
如圖,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于點D,DE⊥AB交AB于點E,AB=4$\sqrt{2}$cm,求△BDE的周長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | C. | 2 $\sqrt{2}$+3$\sqrt{2}$=5$\sqrt{2}$ | D. | $\sqrt{(\sqrt{2}-\sqrt{3})^{2}}$=$\sqrt{2}-\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com