
 校車安全是近幾年社會關注的重大問題,安全隱患主要是超速和超載.某中學數學活動小組設計了如圖檢測公路上行駛的校車速度的實驗:先在公路旁邊選取一點C,再在筆直的車道l上確定點D,使CD與l垂直,測得CD的長等于30米,在l上點D的同側取點A、B,使∠CAD=30°,∠CBD=45°.
校車安全是近幾年社會關注的重大問題,安全隱患主要是超速和超載.某中學數學活動小組設計了如圖檢測公路上行駛的校車速度的實驗:先在公路旁邊選取一點C,再在筆直的車道l上確定點D,使CD與l垂直,測得CD的長等于30米,在l上點D的同側取點A、B,使∠CAD=30°,∠CBD=45°.分析 (1)分別在Rt△ADC與Rt△BDC中,利用正切函數,即可求得AD與BD的長,繼而求得AB的長;
(2)由從A到B用時2秒,即可求得這輛校車的速度,比較與40千米/小時的大小,即可確定這輛校車是否超速.
解答 解:(1)由題意得,
在Rt△ADC中,AD=$\frac{CD}{tan30°}$=$\frac{30}{\frac{\sqrt{3}}{3}}$≈51.9(米),
在Rt△BDC中,BD=$\frac{CD}{tan45°}$=$\frac{30}{\frac{\sqrt{2}}{2}}$≈42.3(米),
則AB=AD-BD≈51.9-42.3=9.6(米);
(2)超速.
理由:∵汽車從A到B用時2秒,
∴速度為9.6÷2=4.8(米/秒),
∵4.8×3600=17280(米/時),
∴該車速度為17.28千米/小時,
∵小于40千米/小時,
∴這輛校車在AB路段不超速.
點評 此題考查了解直角三角形的應用問題.此題難度適中,解題的關鍵是把實際問題轉化為數學問題求解,注意數形結合思想的應用.


科目:初中數學 來源: 題型:解答題
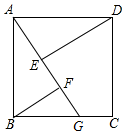 在邊長為4cm的正方形ABCD中,點G是射線CB上的一點,E、F為直線AG上兩個動點,連接DE、BF.
在邊長為4cm的正方形ABCD中,點G是射線CB上的一點,E、F為直線AG上兩個動點,連接DE、BF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
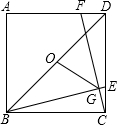 如圖,正方形ABCD中,E,F分別為CD,AD上一點,CE=DF,BE,CF交于點G,O為BD的中點.
如圖,正方形ABCD中,E,F分別為CD,AD上一點,CE=DF,BE,CF交于點G,O為BD的中點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com