
分析 (1)設進購圓規x只,根據三種學具的費用≤3200,列出不等式即可解決問題.
(2)設商店獲得的利潤為y元,進購圓規x只.構建一次函數,理由一次函數的性質即可解決問題.
解答 解:(1)設進購圓規x只,則:10x+18x+4(500-4x)≤3200,
解得:x≤100
∴x至多為100,答:商店至多可以進購圓規100只.…(3分)
(2)設商店獲得的利潤為y元,進購圓規x只.
則y=(13-10)x+(8-6)3x+(5-4)(500-4x)=5x+500,
∵k=5>0,
∴y隨x的增大而增大,
∵x≤100且x為正整數,
∴當x=100時,y有最大值,最大值為:5×100+500=1000,
答:進購100只時,商店獲得的利潤最大,最大利潤為1000元.
點評 本題考查一次函數的應用、一元一次不等式的應用等知識,解題的關鍵是理解題意,學會構建不等式或一次函數解決問題,屬于中考常考題型.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:初中數學 來源: 題型:解答題
 校車安全是近幾年社會關注的重大問題,安全隱患主要是超速和超載.某中學數學活動小組設計了如圖檢測公路上行駛的校車速度的實驗:先在公路旁邊選取一點C,再在筆直的車道l上確定點D,使CD與l垂直,測得CD的長等于30米,在l上點D的同側取點A、B,使∠CAD=30°,∠CBD=45°.
校車安全是近幾年社會關注的重大問題,安全隱患主要是超速和超載.某中學數學活動小組設計了如圖檢測公路上行駛的校車速度的實驗:先在公路旁邊選取一點C,再在筆直的車道l上確定點D,使CD與l垂直,測得CD的長等于30米,在l上點D的同側取點A、B,使∠CAD=30°,∠CBD=45°.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0.15×107 | B. | 0.15×108 | C. | 1.5×107 | D. | 1.5×108 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
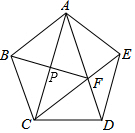 如圖,正五邊形ABCDE中,連接AC、AD、CE,CE交AD于點F,連接BF,BF與AC交于點P.
如圖,正五邊形ABCDE中,連接AC、AD、CE,CE交AD于點F,連接BF,BF與AC交于點P.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
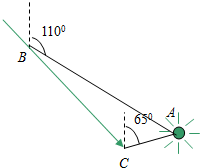 如圖,貨輪在海上自B點沿方位角(指從北按順時針轉到目標線的角度)140°的方向航行,為了確定船位,船在B點觀測燈塔A的方位角為110°,船到達C點,觀測燈塔A的方位是65°,求AB與AC的夾角是多少?
如圖,貨輪在海上自B點沿方位角(指從北按順時針轉到目標線的角度)140°的方向航行,為了確定船位,船在B點觀測燈塔A的方位角為110°,船到達C點,觀測燈塔A的方位是65°,求AB與AC的夾角是多少?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com